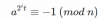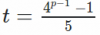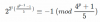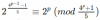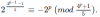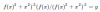-
Chloé Stein Muñoz
el 15/5/17 -
Paula
el 15/5/17 -
Paula
el 15/5/17
Ángel
el 15/5/17Tenemos una función cuadrática (parábola), vamos a buscar el vértice para encontrar los posibles valores máximos y mínimos (en este caso será un mínimo porque 0.1 > 0):
V= -b/(2a)
V= -(-3)/(2*0.1)= 3/(0.2)=15
Entonces, tendremos un mínimo a los 15 días; deducimos entonces que estarán bajando los primeros 15 días y subiendo los sucesivos
También por simetría de la parábola sabemos que cuando transcurran otros 15 días (15 +15=30), en el día 30 el valor se habrá recuperado hasta valer lo mismo que el "día 0"
Sustituyendo el último día (el día 31) en la ecuación parabólica obtendremos que el valor máximo es 0.1*312-93+100= 103.1 en el día 31
El valor mínimo será de 0.1*152-45+100= 77.5 en el día 15
-
Patri Lopez
el 15/5/17 -
Antonio Jesus
el 15/5/17
Como puedo calcular el volumen de esta figura usando Tales?
Ángel
el 15/5/17 -
Guillem De La Calle Vicente
el 15/5/17
Demuestra que
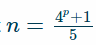es un 2-pseudoprimo fuerte para todos p> 5Quiero demostrar que
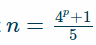es un 2-pseudoprimo fuerte para todos p> 5. Esto significa que n es un número compuesto que pasa la prueba de Miller-Rabin. Es fácil comprobar que es de hecho un compuesto no. Escribimos n-1=2st donde t es un número impar. n pasa la prueba siat≡ 1 (mod n)
o
para algunos i <s.
Entonces
por tanto s=2 y
Asi es
o
?
Comprobé los resultados de los primeros primos (Yup, WolframAlpha ayudó). Resulta que siempre es este último caso el que se mantiene.
Mi conjetura es que:
si p ≡ 3 (mod 4) entonces
si p ≡ 1 (mod 4) entonces
Elevando al cuadrado ambos lados y el resultado sigue. ¿Podría alguien mostrar por qué mi conjetura es correcta (o no?)?
David
el 19/5/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Sara Tarjuelo
el 15/5/17 -
Guillem De La Calle Vicente
el 15/5/17Cómo convertir un valor en un ángulo?
Estoy intentando usar f'(x) en una ecuación donde necesita ser convertida para ser usada como cos(g(f'(x))) donde g(x)=y rad o grados
Lo que estoy trabajando actualmente es conseguir que esta ecuación trabaje con líneas horizontales.
Y eso es lo mismo que f(x) = y
-
Eli
el 15/5/17 -
Mishell Dlc
el 15/5/17En una población de cierta especie de cérvidos, el 43 % de los adultos son machos y el 57 % hembras. Se sabe que el 11 % de los machos adultos y el 4 % de las hembras adultas sufre alguna afección ocular. Se supone que se captura al azar un ejemplar adulto y se pide:
a) (1 punto) Determinar la probabilidad de que tenga alguna afección ocular.
b) (1 punto) Si el ejemplar capturado padeciere una afección ocular ¿cuál sería la probabilidad de que fuera un macho?
Como se haría este con probabilidad con el teorema de bayes es un modelo de examen de selectividad de este año
