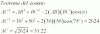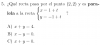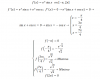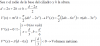-
Cualquier entero en 99, 999, 9999 ... secuencia no es un cuadrado perfecto
Estoy aprendiendo la teoría numérica y tratando de entender cómo es que la siguiente declaración es verdadera.
Demuestre que ningún entero en la siguiente secuencia puede ser un cuadrado perfecto:
99, 999, 9999, 99999, ...
Ángel
el 15/5/17Buenas Guillem!
No he visto información que me confirme lo siguiente (ni tampoco un contraejemplo que lo desmienta) pero te diría observando patrones que:
" Cualquier número de dos cifras o más que sea cuadrado cuadrado perfecto ha de tener, al menos, un número par "
En tu secuencia son todos nueves, números impares.
Comprueba mi afirmación con estos números si quieres:
11,111,1111,11111,111111,....
33,333,3333,33333,333333,....
55,555,5555,55555,555555,....
77,777,7777,77777,777777,....
encontraste cuadrados perfectos entre ellos?
-
alguien me podria decir como hallar la recta paralela a otra en este tipo de ejercicios? no encuentro ejercicios parecidos y no entiendo que este desglosado en y x en vez de ser una sola funcion ... gracias de antemano
-
-
Defina el dominio de la función f(x,y) = (x2 + y )/(x + y2) y haga un bosquejo del mismo. Trace en el mismo gráfico las curvas de nivel que pasan por los puntos (1,-1) y (1,0)
Me pueden ayudar? grafico el dominio, que es una parabola x=-y^2. Pero no entiendo las curvas de nivel, si reemplazo el (1,-1) en la ecuacion, me da 0/2, que es igual a 0, entonces la curva de nivel seria un punto en el 0? Gracias a todos
-
Antonio Silvio Palmitano
el 15/5/17