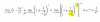-
Antonio Silvio Palmitano
el 14/5/17Tienes la función cuya expresión es:
f(x) = ln(│x2-1│).
Observa que el argumento del logaritmo es positivo (es un valor absoluto), por lo que solo debe cumplirse que dicho argumento sea distinto de cero:
│x2-1│ ≠ 0, que conduce a:
x2-1 ≠ 0, haces pasaje de término y queda:
x2 ≠ 1, haces pasaje de potencia como raíz y tienes dos opciones:
x ≠ - 1 y x ≠ 1.
Por lo tanto, el dominio de la función queda:
D = R - {-1,1} = (-∞,-1) u (-1,1) u (1,+∞).
Espero haberte ayudado. -
En el ejercicio anterior queria saber, de la primmera foto, si lo planteado en rojo esta bn deducido, y de la segunda foto quisiera saber si es negativo porque el signo de la expresión es menor igual (teniendo en cuenta q mi profesor me dio la tabla al reves, es decir el valo del 0,0 es de 0.5000
Por si necesitan el enunciado El nivel medio de colesterol en sujetos obesos es de 248 mg/100 ml y su
desviación típica de 40 mg/100 ml. Tomamos una muestra de 626 obesos.
Teniendo en cuenta que la variable se distribuye normalmente:
a. Calcúlese cuántos sujetos con obesidad de los 626 tendrán el colesterol
superior a 320 mg/100 ml
b. ¿Qué nivel de colesterol será superado por el 75% de la población de obesos?
¿Cómo se llama ese punto?
c. ¿Qué porcentaje de la población de obesos tiene un nivel de colesterol en el
intervalo 208, 288?
d. Hallar dos niveles de colesterol tales que el 95% de la población de obesos
esté entre esos dos valores.
Estudiante 101
el 15/5/17Antonius Benedictus
el 15/5/17 -
Antonio
el 14/5/17Sea e el número de estudiantes y p el precio de la excursión
e·p = 540 si van todos
(e-6)(p+3)=540 si faltan 6 estudiantes
resolviendo el sistema
e=36
p=15
por lo tanto iban 36 estudiantes pagando 15 euros cada uno
solución: fueron 30 estudiantes pagando 18 euros cada uno
p(e)=540/e
20=540/e => e=27 => 27 estudiantes o más
-
no se muy bien como hallar la igualdad a 0 de las derivadas con coseno
g(x) = 6.7sen(0.42x - 0.1) - 0.15
f(x) = 7sen(0.46x - 1.9) + 6.8
estas las derive y me quedaron
f '(x) = 7(cos(0.46x - 1.9)(0.46))
g '(x) = 6.7(cos(0.42x - 0.1)(0.42))
y las volvi a derivar para hallar la derivada segunda
f ''(x) = 1.4812(-sen(0.46x-1.9))
g ''(x) = 1.18188(-sen(0.42x - 0.1))
Tengo que hallar los puntos criticos de la derivada segunda igualandola a 0 y se que seran infinitos puntos porque la funcion es secuencial pero quiero saber el valor maximo que alcanzara infinitas veces como hago
Antonio Silvio Palmitano
el 15/5/17Tienes la expresión de la derivada segunda de la primera función:
g ' ' (x) = - 1,18188*sen(0,42*x - 0,1), luego planteas la condición de punto crítico:
g ' ' (x) = 0, sustituyes y queda:
- 1,18188*sen(0,42*x - 0,1) = 0, haces pasaje de factor como divisor y queda:
sen(0,42*x - 0,1) = 0, compones con la función inversa del seno y queda:
0,42*x - 0,1 = k*π, con k ∈ Z, haces pasaje de término y queda:
0,42x = k*π + 0,1, haces pasaje de factor como divisor y queda:
x = (k*π + 0,1)/0,42, con k ∈ Z, que corresponden a posibles inflexiones en la gráfica de la función g.
Si se trata de plantear la condición de posibles máximos o posibles mínimos en la gráfica de la función g, tienes:
g ' (x) = 0, sustituyes y queda:
6,7*cos(0,42*x - 0,1) = 0, haces pasaje de factor como divisor y queda:
cos(0,42*x - 0,1) = 0, compones con la función inversa del coseno y queda:
0,42*x - 0,1 = (2*n+1)*π/2, con n ∈ Z, haces pasaje de término y queda:
0,42*x = (2*n+1)*π/2 + 0,1, haces pasaje de factor como divisor y queda:
x = ( (2*n+1)*π/2 + 0,1 )/0,42, con n ∈ Z.
Espero haberte ayudado.
-
Hola. En me quede en esta parte, porq no se cual sería la derivada de n/x. Me podrian ayudar oor favor?
-
Antonio
el 14/5/17 -
¿Es la ecuación x³-y³≡k mod n siempre solucionable, cuando ni 7 ni 9 dividen n?
Quería encontrar módulos n, tales que
x³-y³≡k mod nno es solucionable para algunos k.
Para n = 7, no tenemos solución, si k es 3 o 4. Y si n = 9, no tenemos solución si k es 3,4,5 ó 6.
Pero la verificación de los números n = 2 a 500 demostró que siempre existe una solución si ni 7 ni 9 dividen n.
¿Es verdadera la siguiente conjetura?
Si n> 1 y ni 7 ni 9 divide n, entonces la ecuación
x³-y³≡k mod n
es solucionable para todos los k?
Si la conjetura anterior es realmente verdadera esto implica que x³-y³≡z! mod n es siempre solucionable para z≥7 y n> 1?
David
el 19/5/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)