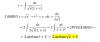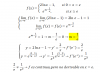-
Usuario eliminado
el 25/4/17Hola, me ayudan ? muchísimas gracias
1-) El punto C (-3,2) es el centro de una elipse, que es tangente a los ejes coordenados. Hallar la ecuación de la elipse, sabiendo que sus ejes son paralelos a los ejes coordenados
2-) Hallar la ecuación de la elipse sabiendo que su excentricidad es e=⅔, uno de sus de sus focos es F(2,1) y la ecuación de la directriz correspondiente x-5=0
-
Sandy Murillo S...
el 25/4/17
Hola estimados de unicoos. Buen día.
Alguien puede por favor ayudarme, los necesito inmensamente. Os ruego ayuda en el problema adjunto, debo hallar las coordenadas del centro (centroide) de la circunferencia mediante integración.
// Demuestre por integración que (h,k) es el centro de la circunferencia dada por la ecuación C: (x-h)2 + (y-k)2 = r2 .
A la persona que me brinde su ayuda, le doy desde yá gracias, del modo mas sincero mil gracias. Saludos...
Antonio Silvio Palmitano
el 25/4/17Comienza por parametrizar la circunferencia C (observa que r es constante, e igual al radio de la circunferencia):
r(t) = < r*cost + h , r*sent + k >, con 0 ≤ t ≤ 2π, en la que sus componentes son:
x(t) = r*cost + h,
y(t) = r*sent + k;
luego, observa que la expresión del vector tangente es:
r ' (t) = < - r*sent , r*cost >,
cuyo módulo es: | r ' (t) | = r.
Luego, planteamos la longitud de la circunferencia: L = 2π*r.
Luego planteamos las integrales de línea:
I1 = ∫c x*ds = ∫ x(t)*| r ' (t) |*dt = ∫ (r*cost + h)*r*dt = r2 ∫ cost*dt + h*r ∫ dt = r2*[ sent ] + h*r*[ t ]= evaluamos =
= r2*( sen(2π) - sen(0) ) + h*r*(2π - 0) = r2*0 +h*r*2π = 0 + 2π*h*r = 2π*h*r.
I2 = ∫c y*ds = ∫ y(t)*| r ' (t) |*dt = ∫ (r*sent + k)*r*dt = r2 ∫ sentt*dt + k*r ∫ dt = r2*[ - cost ] + k*r*[ t ]= evaluamos =
= r2*( - cos(2π) - (- cos(0) ) + k*r*(2π - 0) = r2*(- 1 + 1) +k*r*2π = r2*0 + 2π*k*r = 0 + 2π*k*r = 2π*k*r.
Luego, planteamos las coordenadas del centroide:
xc = I1/L = sustituimos = (2π*h*r)/(2π*r) = simplificamos = h.
yc = I2/L = sustituimos = (2π*k*r)/(2π*r) = simplificamos = k.
Espero haberte ayudado.
-
Candela
el 25/4/17 -
andres
el 25/4/17 -
andres
el 25/4/17 -
Jacobo VillaVerde Martinez
el 25/4/17hola me podíais ayudar con este problema de probabilidad Gracias
El 45 % de los alumnos de un Instituto son mujeres. El 24 % de los varones repite curso y el 30 % de las mujeres también. Calcular la probabilidad de que, al elegir un estudiante al azar,
a) sea varón y repetidor.
b) sea mujer y no repita curso.
c) sea mujer, sabiendo que es repetidor. -
Veronica montenegro
el 25/4/17sea la funcion f : D ⊂ R2 → R definido como f (x, y) =y2/x, hallar su dominio
porfa ayuda
Antonio Silvio Palmitano
el 25/4/17Si la función tiene la expresión: f(x,y) = y2/x, observa que es una expresión algebraica fraccionaria, por lo que la única condición a tomar en cuenta es que el denominador debe ser distinto de cero, por lo tanto tienes: D = { (x,y) ∈ R2: x ≠ 0 }, y observa que, gráficamente, el dominio comprende a todos los puntos del plano OXY, excepto los puntos del eje coordenado OY.
espero haberte ayudado.
-
Fernando Cordoba Espada
el 25/4/17buenas, tengo problemas con algunos ejercicios ya que no se hallar el baricentro del area encerradq por una función:
Determina el baricentro del recinto encerrado por y = sen(x) con el eje 0X en el intervalo [0, π/2].
Antonius Benedictus
el 25/4/17
Fernando Cordoba Espada
el 25/4/17
Antonio Silvio Palmitano
el 25/4/17Observa que puedes describir la Región (R) en dos formas diferentes:
1) 0 ≤ y ≤ senx, con 0 ≤ x ≤ π/2, como tienes en tu enunciado;
2) arcseny ≤ x ≤ π/2, con 0 ≤ y ≤ 1.
Luego, tienes que el área de la región es:
A = ∫ (senx - 0)*dx = [ - cosx ] = evaluamos = - cos(π/2) - ( - cos(0) ) = - 0 + 1 = 1.
Luego, planteamos:
I1 = ∫ x*senx*dx = te dejo la resolución (puedes aplicar el método de integración por partes).
Luego plantamos:
I2 = ∫ y*(π/2 - arcseny)*dy = te dejo la resolución (puedes separar en términos, y el primero es de resolución directa y el segundo lo puedes resolver por partes).
Luego, las coordenadas del baricentro quedan:
xb = I1/A,
yb = I2/A.
Espero haberte ayudado.
-
Nico Demo
el 25/4/17Necesito solucionar un ejercicio de las relaciones de conjuntos y sus propiedades de
desigualdades y exponentes (comprobar si es simétrica, transitiva y reflexiva).
Ángel
el 25/4/17Sin asegurarte nada, creo que los pares que componen R son:
(1,2), (1,3), ............
(2,2), (2,3), ............
(3,2), (3,3).........
..
(descartamos sólo los pares (a,b) en los que b=1
No es simétrica: Si el 1º está relacionado con el 2º, TAMBIÉN VICEVERSA......por ejemplo está el (1,3) pero no el (3,1) .....
Sí es transitiva: Si el 1º está relacionado con el 2º y el 2º con el 3º, entonces el 1º está relacionado con el 3º
No es reflexiva: Para que sea reflexiva tiene que cumplirse que cada elemento está relacionado consigo mismo...se cumple (2,2), (3,3),(4,4), (5,5)...........pero no está en la relación el (1,1)
-
Julian Jerez
el 25/4/17
