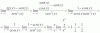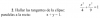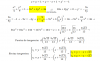-
Ingrid
el 31/3/17Me puden ayudar con la conversiòn 386 in/s2 a m/s2
in: pulgada
s2: segundo al cuadrado
Ángel
el 31/3/17
Antonio Silvio Palmitano
el 31/3/17Recuerda la equivalencia entre pulgada y metro: 1 in = 0,0254 m.
Luego, solo tienes que multiplicar por 0,0254 para pasar de pulgadas a metros, y tienes que dividir por 0,0254 para pasar de metros a pulgadas.
Luego vamos a tu cálculo:
386 in/s2 = 386*0,0254 m/s2 = 9,8044 m/s2.
Espero haberte ayudado.
Iswag Newton
el 31/3/17 -
Patri Lopez
el 31/3/17
podeis resolverme el 29 y 34, los he hecho un montón de veces y no hay manera de que me salga el resultado.. un saludo y muchísimas gracias -
Osmaynis Derken González
el 31/3/17
Tengo una duda cuando voy a multiplicar el resultante con la matriz de 2x2 ,resulta que el resultante es de 3x3 ,se puede multiplicar matrices de diferente dimesion ,sera que me puedan explicar ,
yo hice esto:
Guillem De La Calle Vicente
el 31/3/17Guillem De La Calle Vicente
el 31/3/17Dada la primera imagen, creo que tienes que calcular el producto booleano en comparación con el producto Tensor:
Mirando la primera foto, parece que usted necesita calcular el producto booleano. El cálculo de esto es lo mismo que calcular un producto regular de dos matrices excepto que los + denotan disyunción (OR) y los ⋅ denotan conjunción (AND) como hacen normalmente en el álgebra booleana. Puesto que usted tiene el producto de una matriz 3 × 2 y una matriz 2 × 2, la matriz resultante será 3 × 2.
Si A es la primera matriz, B es la segunda y C es el producto booleano de los dos, entonces el elemento en la fila i columna j de C será el producto de punto booleano de la fila i en A con la columna j en B.
-
Stiven
el 31/3/17 -
Stiven
el 31/3/17Alguien puede decirme si esta bien está derivada?
Ángel
el 31/3/17La primera te la mandó Antonio, la segunda: y=3x2/x2 te complicaste la vida, pues quedaría y=3
x2/x2 ------> y=3 ====> y´=0Y si por algún casual la quisieras hacer sin eliminar el elemento común x2, tendrías que seguir simplificando en tu derivada (te quedaste a medias)
(6x*x2 - 3x2*2x)/(x2)2=
(6x3 - 6x3)/x4=
0/x4=
0
-
Patri Lopez
el 31/3/17
alguien puede resolverme estos dos limites? No me salen 😣😥😥 muchas gracias🤗🤗
David
el 17/4/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Patri Lopez
el 31/3/17- alguien puede encontrarme el fallo??
Patri Lopez
el 31/3/17
Antonius Benedictus
el 31/3/17Guillem De La Calle Vicente
el 31/3/17 - alguien puede encontrarme el fallo??
-
Pablo Molina
el 31/3/17Buenas, he encontrado este ejercicio, y me gustaría saber el procedimiento para resolverlo, he intentado hacer un sistema con ambas ecuaciones pero no me ha salido nada.
Me dan dentro de la elipse, pero no parece que pueda pasar una recta con m=-1 por ahí, la verdad.
-
Amparo Armenteros
el 31/3/17Por favor, podrían ayudarme con esta pregunta:
Halla k para que r: (k+5)x - (3+k)y = 1-k pase por el punto P(2,3)
-
Brayan
el 31/3/17
