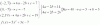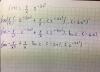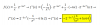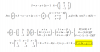Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Osmaynis Derken González
el 31/3/17

Hola sera que me puedan ayudar, la he echo y siempre me termino enredando así como la tengo ahí esta mala creo
lo he echo con plano cartesiano ,pero no se como acomodar la parábola, de antemano gracias por la ayuda,

••0 voto/s
•
César
el 31/3/17

•1 voto/s
•

Cancelar
Luciano De Renzo
el 31/3/17

Buenas noches, estoy intentando hacer una derivada y entiendo que me salió pero siempre se me complica bastante simplificar y operar despues. Llegue hasta ese punto y probe algunas cosas pero no llego al resultado correcto que es f'(x)=(x^-2+6ln2).(-2^-3x^2) Gracias.

••0 voto/s
•
Antonius Benedictus
el 31/3/17

•0 voto/s
•

Cancelar
Diego
el 31/3/17

¿Puede alguien explicarme como hacer estos ejercicios? O al menos el numero 7, por favor.

••0 voto/s
•
Antonius Benedictus
el 31/3/17

•1 voto/s
•
Diego
el 31/3/17
muchas gracias!!

•0 voto/s
•

Cancelar
Bruno
el 31/3/17

Me podrian ayudar con la sig integral porfavor

••0 voto/s
•
Antonius Benedictus
el 31/3/17

•0 voto/s
•
César
el 31/3/17

•0 voto/s
•

Cancelar
Lola
el 31/3/17

Hola,como se resuelve esto paso a paso? Es de fisica pero no responde nadie! Muchas gracias!
Una pelota es arrojada hacia arriba desde 3m de altura con una velocidad de 60m/seg,tres segundos mas tarde es arrojada hacia arriba otra pelota en la misma vertical desde 8 m de altura con una velocidad de 70 m/seg.¿En que instante y a que altura las dos pelotas se chocan?

••0 voto/s
•
César
el 31/3/17

•0 voto/s
•

Cancelar
Camila Tey
el 31/3/17

Hola chicxs, tengo un libro llamado " Libros de Matemática a Medida" de Ediciones Logikamente. Esta bueno, lo pueden bajar de internet. Para los que están en secundario o terciarios es re re util. Ami me re sirvió .

••3 voto/s
•
David
el 17/4/17
:D Gracias!

•0 voto/s
•

Cancelar
Meiko Benegas
el 31/3/17

Gente, como halló un punto que pertenezca a la recta??
El enunciado me dice que halle las ecuaciones de recta a partir de éste dato:
Es la recta intersección de los planos 3x + 2y - 4z - 6 = 0 y x - 3y - 2z - 4 = 0.

••0 voto/s
•
Gianluca
el 31/3/17
¿Y te dan algún vector director o pendiente en concreto?

•1 voto/s
•
Antonius Benedictus
el 31/3/17

•1 voto/s
•
Meiko Benegas
el 31/3/17
No, o sea el vector dirección lo puedo sacar del vector normal de alguno de los dos planos, pero no sabía cómo encontrar un punto que pertenezca a la recta con los datos que me daban de los planos

•1 voto/s
•

Cancelar
Daniel Tennant
el 31/3/17

Como encuentro el rango de esta función? g(x)= 5 / 2x+3 Gracias

••0 voto/s
•
Ángel
el 31/3/17
g(x)= y= 5/(2x+3)

1er paso) Despejamos la x de la función g(x) o lo que es lo mismo: y
y= 5/(2x+3)
y*(2x+3)=5
2x+3= 5/y
2x= (5/y)-3
x=[(5/y)-3]/2
x=(5/2y)-(3/2)
x=(5-3y)/2y

2º paso) Cambiamos las y por x en la función del paso anterior
(5-3x)/2x

3er paso) Calculamos el dominio de lo obtenido en el paso anterior (O LO QUE ES LO MISMO, LA INVERSA)
Se trata de una función racional con numerador y denominador de tipo polinómicos (por separados el dominio sería todo R), pero al ser racional en su conjunto tenemos que ver los valores que anulen el denominador y por tanto, indeterminen la función. Lo hacemos:
Denominador: 2x
2x=0
x= 0/2= 0

DE ESTO CONCLUIMOS QUE EL RANGO DE g(x) ES TODO R EXCEPTO EL CERO (QUE ES EL VALOR QUE INDETERMINA LA FUNCIÓN DE LA FUNCIÓN INVERSA)
RANGO= (-INF,0) U (0,INF)= R- {0}

•1 voto/s
•
Daniel Tennant
el 31/3/17
MUCHAS GRACIAS!!

•0 voto/s
•

Cancelar
Hans Beckenbauer
el 31/3/17

ayuda porfavor, ¿como resolveria esta operación?

••0 voto/s
•
Ángel
el 31/3/17
[log₃(27-x³)]/[log₃(3-x)] = 3

log₃(27-x³) = 3*[log₃(3-x)]

log₃(27-x³) = [log₃(3-x)³]

~~log₃~~(27-x³) = ~~log₃~~(3-x)³

(27-x³) = (3-x)³
Continúa tú desarrollando el producto notable (3-x)³, te recomiendo que si no te lo sabes lo busques...obtendrás el valor o valores de x, tendrás que verificar estas soluciones o valores en la ecuación original y así concluir qué valores hacen verdadera nuestra igualdad.

Y si sigues atascado, vuelve a consultar.

•1 voto/s
•
Hans Beckenbauer
el 31/3/17
lo rehice y me quedo asi
•0 voto/s
•
Ángel
el 31/3/17
Va de lujo...terminamos:
-9x²+27x=0
9x²-27x=0
9(x²-3x)=0
x²-3x=0
x(x-3)=0
x₁=0
x₂-3=0----> x₂=3

Por último comprobamos que cuando x es sustituida por x₁ en [log3(27-x3)]/[log3(3-x)] = 3
esto nos queda:
[log3(27-03)]/[log3(3-0)] = 3
(log33³)/(log33) = 3
3/1=3
3=3 VERDADERO
Por lo tanto, x=0 es una solución válida

En cambio, si hacemos x=3 en [log3(27-33)]/[log3(3-3)] = 3
[log3(0)]/[log3(0)] = 3 FALSO, ya que el log_n0 no está definido

Por lo tanto, la única solución es x=0

•1 voto/s
•

Cancelar