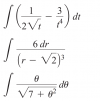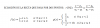-
Antonio Silvio Palmitano
el 25/3/17Vamos con orientaciones.
1) Puedes expresar el integrando en la forma: f(t) = (1/2)t-1/2 - 3t-4, para luego separar en términos, extraer factores constantes, e integrar en forma directa.
2) Puedes aplicar la sustitución (cambio de variable): w = r - √(2), de donde tienes: dw = dr, luego sustituyes, extraes el factor constante y la integral para resolver queda:
6*∫w-3dw, que puedes integrar en forma directa.
3) Puedes aplicar la sustitución: w = 7 + θ2, de donde tienes: dw = 2*θ*dθ, y luego tienes: (1/2)*dw = θ*dθ, luego sustituyes, extraes el factor constante y la integral para resolver queda:
(1/2)*∫w-1/2dw, que puedes integrar en forma directa.
Queda para que concluyas la tarea.
Espero haberte ayudado.
-
Guillem De La Calle Vicente
el 25/3/17A ∪ B = B ∪ A
Si x es cualquier elemento de A ∪ B después, por la definición de unión, tenemos que x ∈ A o x ∈ B. Pero, si x es en A o B, después está en B o A, y por definición de unión, eso significa que x ∈ B ∪ A. Por tanto, A ∪ B ⊆ B ∪ A.
La otra inclusión es identica: si x es cualquier elemento de B ∪ A, después sabemos que x ∈ B o x ∈ A. Pero, x ∈ B o x ∈ A implica que x está en A o B, por tanto, x ∈ A ∪ B. Por esta razón, B ∪ A ⊆ A ∪ B.
Por tanto, A ∪ B = B ∪ A.
A ∩ B = B ∩ A
Si x es cualquier elemento de A ∩ B, después sabemos por la definición de intersección que x ∈ A y x ∈ B. Por tanto, x ∈ B y x ∈ A, y eso implica x ∈ B ∩ A. Por tanto, A ∩ B ⊆ B ∩ A.
La inclusión inversa es otra vez identica: si x es cualquier elemento de B ∩ A, después sabemos que x ∈ B y x ∈ A. Por tanto, x ∈ A y x ∈ B. Eso implica que x ∈ A ∩ B. Por tanto, B ∩ A ⊆ A ∩ B.
Por tanto, A ∩ B = B ∩ A.
Antonio Silvio Palmitano
el 25/3/17Vamos con una orientación: debes tener en cuenta las definiciones de las operaciones entre conjuntos:
1) ∀x: x ∈ A ∪ B
x ∈ A ∪ B ↔ x ∈ A ∨ x ∈ B ↔ x ∈ B ∨ x ∈ A ↔ x ∈ B ∪ A, por lo tanto concluyes: A ∪ B = B ∪ A,
observa que hemos aplicado: definición de unión, conmutatividad de la disyunción, definición de unión.
2) ∀x: x ∈ A ∩ B
x ∈ A ∩ B ↔ x ∈ A ∧ x ∈ B ↔ x ∈ B ∧ x ∈ A ↔ x ∈ B ∩ A, por lo tanto concluyes: A ∩ B = B ∩ A,
observa que hemos aplicado: definición de intersección, conmutatividad de la conjunción, definición de intersección.
Espero haberte ayudado.
-
Ángel
el 25/3/17Ángel
el 25/3/17 -
Darío
el 25/3/17Darío
el 25/3/17 -
Hola, mi duda en concreto es sobre un ejercicio de estadística
Se han medido las pulsaciones a un grupo de pacientes tras una prueba de esfuerzo:
Pulsaciones Nº de pacientes
65-69 0
70-74 3
75-79 3
80-84 7
85-89 10
90-94 12
95-99 8
Mi duda era, si los intervalos los debo coger cerrados no?, porque es así como me dan las clases de datos?
Y otra duda era si el intervalo modal es la moda, gracias :)
Antonio
el 25/3/17Antonio Silvio Palmitano
el 25/3/17Los intervalos son cerrados, por ejemplo el primero expresado por extensión es: {65, 66, 67, 68, 69], y el segundo expresado por extensión es: {70, 71, 72, 73, 74}, y observa que si los considerásemos abiertos, quedarían valores sin contemplar, que serían: 65, 69 y 70, 74 y 75, 79 y 80, ... 94 y 95, y 99.
Y tal cuál afirmas, el intervalo modal es el anteúltimos: [90,94], cuya frecuencia es 12, que es la mayor entre las frecuencias de todos los intervalos.
Espero haberte ayudado.
-
Ángel
el 25/3/17Antonius Benedictus
el 25/3/17Andrea
el 25/3/17Ángel
el 25/3/17Por norma general, y como paso lógico en el proceso de resolución, te diría que radicalizar: esto es, multiplicar por dicha raíz perteneciente al denominador en el propio denominador y en el numerador, así esa raíz la tendrás arriba para operar más cómodamente
Mándanos un pantallazo del problema concreto
Antonius Benedictus
el 25/3/17 -
Buenos dias me podriais ayudar?
Ejercicio 1º
Sea la función: f(x)= -x+3 si x<3
x-3 si x≥3
Dibujar la gráfica de la función ( No se como dibujarla )y estudiar la continuidad y derivabilidad en x=3(2,5 puntos)
Ejercicio 2º
- Hallar la ecuación de la recta tangente a la gráfica de la función f(x) = x3 – 2x2 en el punto de coordenada x=1
- Hallar la ecuación de la recta normal la gráfica de la función f(x) = 3x2 – 4x en el punto de coordenada x=2