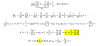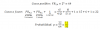-
Ángel
el 25/3/17Judit
el 25/3/17 -
-
Podrías ayudarme?
Ejercicio 3º
Calcular la derivada de las siguientes funciones:
a) y= x elevado a la 2 por e elevado a la x
b) y= 1/2x
c) y= 2x elevado a la 4-5x elevado a la 3+ 3x elevado a la 2-2
d) y= x elevado a la 2+3/ elevado a la 2-1
e) y=√x por ln(x)
ros
el 25/3/17Antonio
el 25/3/17 -
si se lanzan 6 monedas iguales al aire cual es la probabilidad de que salgan 4 o mas caras?
gracias
Antonio Silvio Palmitano
el 25/3/17Definimos la variable aleatoria discreta: X: "cantidad de caras obtenidas al arrojar seis monedas equilibradas al aire", cuyos valores pertenecen al conjunto: VX = {0, 1, 2, 3, 4, 5, 6], cuya distribución de probabilidad es binomial con parámetros: n = 6, p = 1/2, q = 1/2, cuya expresión es:
p(X = k) = C(6,k)*(1/2)k*(1/2)6-k = C(6,k)*(1/2)k+6-k = C(6,k)*(1/2)6 = (1/64)*C(6,k).
Luego, tenemos el suceso: S: "se obtuvieron 4 o más caras", cuya probabilidad planteamos:
p(S) = p(X ≥ 4) = p(X = 4) + p(X = 5) + p(X = 6) =
= (1/64)*C(6,4) + (1/64)*C(6,5) + (1/64)*C(6,6) = (1/64)*( C(6,4) + C(6,5) + C(6,6) ) =
= (1/64)*(15 + 6 + 1) = (1/64)*22 = 11/32 = 0,34375.
Espero haberte ayudado.
-
Me podeis ayudar porfavor?
Ejercicio 2º
- Hallar la ecuación de la recta tangente a la gráfica de la función f(x) = x3 – 2x2 en el punto de coordenada x=1
- Hallar la ecuación de la recta normal la gráfica de la función f(x) = 3x2 – 4x en el punto de coordenada x=2
Antonio
el 25/3/17Sabemos que la ecuación de la recta es de la forma: y=yo+m(x-xo) donde P(xo, yo) es un punto de la misma y m su pendiente,
por otro lado m=f'(xo)
y las rectas perpendiculares tienen que m=-1/m' siendo m y m' las pendientes respectivas
a)
f(x)=x3 – 2x2
f(1)=-1
f'(x)=3x2-4x
f'(1)=-1
la recta tangente es: y=-1-(x-1)
b)
f(x)=3x2 – 4x
f(2)=4
f'(x)=6x-4
f'(2)=8
m=-1/8
y la recta normal es: y=4-1/8·(x-2)
-
¿Alguien me dice como se hace el ejercicio de hallar la recta tangente y normal de la f(x) = |x^2-4|? Si no estuviera el valor absoluto sabría hacerlo...
Antonius Benedictus
el 25/3/17Antonio
el 25/3/17Sabemos que la ecuación de la recta es de la forma: y=yo+m(x-xo) donde P(xo, yo) es un punto de la misma y m su pendiente,
por otro lado m=f'(xo)
y las rectas perpendiculares tienen que m=-1/m' siendo m y m' las pendientes respectivas
f(x)=4-x^2
f(-1)=3
f'(x)=-2x
f'(-1)=2
la recta tangente es: y=3+2(x+1)
y la recta normal es: y=3-1/2·(x+1)
Antonio Silvio Palmitano
el 25/3/17Debes considerar la expresión a trozos de la función (revisa en tus apuntes de clase):
f(x) =
x2 - 4 si x ≤ - 2 ∨ x ≥ 2
- x2 + 4 si - 2 < x < 2
Luego, observa que la función tiene dominio D = R, que es continua en todo su dominio, y observa también que la función des derivable en todo su dominio, con excepción de x = - 2 y x = 2.
Luego, la expresión de la función derivada queda:
f ' (x) =
2x si x < - 2 ∨ x > 2
- 2x si - 2 < x < 2.
Luego, observa que la gráfica de la función admite recta tangente y admite recta normal en todos sus puntos, con excepción de los puntos (-2,0) y (2,0), para cuyas abscisas no está definida la función derivada.
Luego, solo es cuestión de observar a cuál de los dos trozos corresponde el punto de contacto entre la gráfica de la función, su recta tangente y su recta normal.
Espero haberte ayudado.