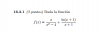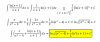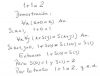-
Marest
el 21/3/17 -
Matemáticas
el 21/3/17
Sea a un número real positivo. Demuestra de forma directa y por el contrarecíproco que si a < 1, entonces a2 < a.
Antonio
el 21/3/17forma directa
a < 1
como a≠0, pues a un número real positivo, podemos multiplicar por a en ambos términos sin variar la desigualdad:
a·a < a·1
a2 < a
contrarrecíprocosi a2 ≥ a
como a≠0, pues a un número real positivo, podemos dividir por a en ambos términos sin variar la desigualdad:
a2/a ≥ a/aa ≥ 1 -
Marest
el 21/3/171.- Determina la longitud de los lados de un triángulo equilátero cuyo área mide 4 cm2.
2.- Cuánto mide la superficie de un octógono regular inscrito en un cuadrado de 4 m de lado?
3.- La rueda de una bicicleta tiene 40 cm de diámetro. ¿Cuántos metros habrá recorrido después de 35 vueltas?
4.- Halla el área de una pista de patinaje circular rodeada por una valla 120 m.
5.- Calcula la longitud de un arco de 120º en una circunferencia cuyo radio mide 8 cm. ¿Cuál es el área del sector circular correspondiente?
Muchísimas gracias por vuestra ayuda.
Ángel
el 22/3/172)
Primero averiguamos el lado, para ello usamos esta formula donde n =cantidad de lados:
Lado= 2 * Radio * seno(π/n)
lado= 2 * 4m * sen (180º/8)
lado= 8m * sen(22º 30')
lado= 8m * 0,38
lado= 3,04m
área= 1/4 * n * Lado2 / tan(π/n)
área= 1/4 * 8 * (3,04m)2 / tan(180º/8)
área= 1/4 * 8 * 9,2416m2 / tan(22º 30')
área= 2* 9,2416m2 / 0,41
área= 18,4832m2 / 0,41
área= superficie= 45,081m2
Ángel
el 22/3/17
Ángel
el 22/3/17 -
Valentina
el 21/3/17 -
Matemáticas
el 21/3/17Sean a y b dos números reales. Demuestra que si a/b es irracional, entonces a o b es irracional. Hazlo por el contrarecíproco o por reducción al absurdo, indicando el método utilizado. Finalmente, investiga si es cierta la afirmación recíproca.
Antonio
el 21/3/17a)
por el contrarrecíproco:
supongamos que a y b son ambos racionales, entonces a/b será racional pues:
a=p/q racional
b=r/s racional
a/b=(p/q)/(r/s)=(ps)/(qr)=m/n racional
b)
la afirmación recíproca es falsa:
el cociente de dos números irracionales no siempre es irracional
como contraejemplo:
a=2π irracional
b=π irracional
a/b=2 natural
-
Hanna
el 21/3/17hola a todos,¿podéis corregirme este ejercicio de tablas de frecuencias?
Hanna
el 21/3/17En x sub i esta muy insatisfecho,insatisfecho,normal,satisfecho y muy satisfecho.
En n sub i esta 15,25,28, 20,12 y de total 100.
En f sub i hay 0´15,0´25,0´28,0´20,0´12 y de total 1.
En N sub i esta 15,40,68,88 y total 100.
En F sub i hay 0´15,0´40,0´68,0´88 y total 1.
En f sub i de poercentaje esta 15%,25%,28%,20%,12% y de total 100%.
-
Matemáticas
el 21/3/17Sea n un número natural. Demuestra de forma directa y por el contrarecíproco que si n3 es múltiplo de 3, entonces n es múltiplo de 3.
Antonio
el 21/3/17Antonio
el 21/3/17por el contrarrecíproco hay que demostrar que si n no es múltiplo de 3, entonces n3 no es múltiplo de 3:
si n no es múltiplo de 3 entonces n no es igual a 3 multiplicado por un número, es decir,bien
n es igual a 3 multiplicado por un número +1
bien
n es igual a 3 multiplicado por un número +2
en el primer caso:
n=3k+1
n3=(3k+1)3=27k3+27k2+9k+1=3(9k3+9k2+3k)+1=3m+1 => no es múltiplo de tres
en el segundo caso:
n=3k+2
n3=(3k+2)3=27k3+54k2+36k+8=3(9k3+18k2+12k+2)+2=3m+2 => no es múltiplo de tres
-
Sonia Ramis García
el 21/3/17ayudita con la pregunta b?
Antonio
el 21/3/17 -
Francisco Javier Fernández
el 21/3/17Hola a tod@s.
Soy un poco bruto en matemáticas y hay cosas que se me escapan, como es el caso de esta demostración: 1 + 1 = 2, que encontré en una foto de un pizarrón...
Si alguien puede explicármela con un poco más de detalle le estaré agradecido.
Gracias por vuestra paciencia.
Antonius Benedictus
el 21/3/17
César
el 21/3/17No es tan sencillo , se necesitaron mas de 300 hojas para demostrarlo http://www.uhu.es/francisco.moreno/gii_mac/docs/Principia_Mathematica_vol3.pdf
La tuya se la dejo a los mas expertos.
Francisco Javier Fernández
el 21/3/17Gracias por contestar.
Es cierto que excede el nivel, no pensé en la demostración "sesuda", sino en la notación usada en el pizarrón en sí, que tiene una parte que no logro seguir...
De todos modos, ya que estoy, cambiando un poco de tema, en los axiomas de Peano se incluye el 0 entre los números naturales, pero yo siempre he creído que no estaba incluido, incluso cuando preparaba el curso de acceso de la UNED pensaba que lo tenía claro: según "Matemáticas especiales", pero ahora ya no sé si lo está o no...
