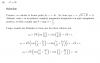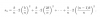-
Alba
el 22/3/17
-
Alumna
el 22/3/17Hola Unicoos, necesito ayuda con este problema, lo he hecho, espero que me podáis ayudar...
Además de indicarme en qué fallo, o si me va bien, os agradecería si me podéis decir qué puedo poner para poder visualizar vídeos de este tipo para poder ayudarme.
Muchas Gracias.
Os dejo el enunciado, dice así:
-Un estudiante recibe 600 € al mes.
Debe pagar un 20% de alquiler de esa cantidad .De la cantidad restante destina cada mes el 50% a comprar comida, el 25% a comprar ropa y otro 25% a salir y gastos varios.
Un día sale de compras y gasta 40 € en unos pantalones, 10 € en comer en un bar, 2 € en el bus y 3 € en consumiciones
¿Qué porcentaje ese día de cada epígrafe? (alquiler, comida, ropa y salir)
Ángel
el 22/3/17Tienes otros 3 o 4 vídeos de resolución de problemas
Pon el enunciado original para que podamos ayudarte
Alumna
el 22/3/17Un estudiante recibe 600 € al mes.
Debe pagar un 20% de alquiler de esa cantidad .De la cantidad restante destina cada mes el 50% a comprar comida, el 25% a comprar ropa y otro 25% a salir y gastos varios.
Un día sale de compras y gasta 40 € en unos pantalones, 10 € en comer en un bar, 2 € en el bus y 3 € en consumiciones
¿Qué porcentaje ese día de cada epígrafe? (alquiler, comida, ropa y salir)
-
Daniel Andrés
el 22/3/17Alguno que me aclare de donde sale la respuesta al argumento que da Pi/medios
Según lo que sé, es que el procedimiento para hallar el valor seria el arctan (0/8) (Supongo que estoy en lo correcto). pero me daria un valor de 0 , entonces no entiendo porque es pi/medios -
Matemáticas
el 22/3/17Me podeis ayudar con este ejercicio. Al principio os pongo la parte a que hace referencia el ejercicio y despues el ejercicio en si.
El ejercicio es:
Guillem De La Calle Vicente
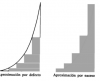
el 22/3/17Las siguientes gráficas muestran las sumas inferior y superior, respectivamente:
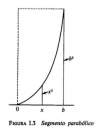
Por lo tanto, ahora tenemos que calcular las sumas inferiores y superiores. Para las sumas más bajas, sumamos el área de todo el rectángulo azul. Cada rectángulo tiene la anchura b/n (ya que hemos dividido el intervalo [0, b] en n partes iguales) y su altura es el valor de la curva en el lado izquierdo del rectángulo (ya que la curva es Dibujado de manera que la esquina izquierda descansa sobre la curva). Por lo tanto, tenemos
Para las sumas superiores, la anchura de cada rectángulo sigue siendo b/n, pero la altura se da ahora por el valor de la función en la esquina derecha. Entonces tenemos,
![\[ S_n = \frac{b}{n} \cdot 2 \left( \frac{b}{n} \right)^2 + \frac{b}{n} \cdot 2 \left( \frac{2b}{n} \right)^2 + \cdots + \frac{b}{n} \cdot 2 \left( \frac{(n-1)b}{n} \right)^2 + \frac{b}{n} \cdot 2 \left( \frac{bn}{n} \right)^2. \]](http://13997-presscdn-0-70.pagely.netdna-cdn.com/wp-content/ql-cache/quicklatex.com-f99d7b65bb006f31aa7c69d4da31fec7_l3_thumb.svg "Rendered by QuickLaTeX.com")
Ahora, se nos da la identidad
![\[ \sum_{i=1}^n i^2 = \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}, \]](http://13997-presscdn-0-70.pagely.netdna-cdn.com/wp-content/ql-cache/quicklatex.com-514d7726c4500406a41737e87bc8261d_l3_thumb.svg "Rendered by QuickLaTeX.com")
Y así, siguiendo el ejemplo de Apostol,
![\[ 1^2 + 2^2 + \cdots + (n-1)^2 < \frac{n^3}{3} < 1^2 + 2^2 + \cdots + n^2. \]](http://13997-presscdn-0-70.pagely.netdna-cdn.com/wp-content/ql-cache/quicklatex.com-a7e04f565f0f6d5510d358d95925eefe_l3_thumb.svg "Rendered by QuickLaTeX.com")
Ahora, multiplicamos cada término en la desigualdad por \ frac {b} {n} \ cdot 2 \ izquierda (\ frac {b} {n} \ derecha) ^ 2 así las sumas en la extrema izquierda y la extrema derecha se convierten en nuestra s_n Y S_n arriba, y podemos simplificar el término en el medio. Así, para todo n \ geq 1 tenemos
Ahora, debemos mostrar que si s_n <A <S_n para todo n \ geq 1 entonces A = \ frac {2b ^ 3} {3}. Logramos esto mostrando que A <\ frac {2b ^ 3} {3} y A> \ frac {2b ^ 3} {3} conducen a contradicciones.
Supongamos que A <\ frac {2b ^ 3} {3}. Entonces, como S_n - s_n = \ frac {2b ^ 3} {n} podemos calcular,
Sin embargo, esto no puede mantenerse para todos los n \ geq 1 ya que el término a la derecha es una constante (dependiendo de b), por lo que siempre podemos elegir un n que sea mayor ya que los enteros positivos son ilimitados arriba.
A continuación, supongamos A> \ frac {2b ^ 3} {3}. Entonces,
Pero, nuevamente, esto no puede ser cierto para todos los enteros positivos n ya que los números enteros positivos son ilimitados arriba. Por lo tanto, tanto A <\ frac {2b ^ 3} {3} y A> \ frac {2b ^ 3} {3} conducen a contradicciones. Por lo tanto, debemos tener
![\[ A = \frac{2b^3}{3}. \qquad \blacksquare \]](http://13997-presscdn-0-70.pagely.netdna-cdn.com/wp-content/ql-cache/quicklatex.com-6b1ea7298730e94a3e3fcf5bf6a08bb5_l3_thumb.svg "Rendered by QuickLaTeX.com")
-
María
el 22/3/17 -
Pilar
el 22/3/17 -
Froylan
el 22/3/17alguien me puede ayudar con este problema:
al abordar un taxi el cobro es de $8.00 y aumenta $1.50 por cada 200 metros recorridos
1- supòn que tus recorridos sòlo abarcan mùltiplos de 200 metros. ¿ cuàl serìa el modelo/funciòn para esta situaciòn?
-
Beatriz
el 22/3/17Los márgenes de un río tienen por ecuaciones: x - y = 2, x - y = -2. Dos pueblos A(-3, 2) y B(4, 0), se van a unir por una línea de ferrocarril que cruzará el río perpendicularmente. ¿En qué puntos de ambas orillas se construirá el puente para que el trayecto sea mínimo?
¿CÓMO PUEDO RESOLVERLO? AYUDA!! URGENTE.
Antonio
el 22/3/17Sea P(a,b) el punto en una orilla y Q(c,d) el punto en la otra orilla
Al estar los dos puntos en perpendicular a ambas rectas tenemos que: Q(b,a)
Además b=a+2, por estar en la primera recta
Entonces P(a,a+2) y Q(a+2,a)
La distancia entre A(-3,2) y P(a,a+2) es √[(a+3)2+(a)2]
La distancia entre B(4,0) y Q(a+2,a) es √[(a-2)2+(a)2]
Sea d(a) la distancia que hay que cubrir de carretera
d(a)=√[(a+3)2+(a)2] +√[(a-2)2+(a)2]
minimizar la distancia entre los dos pueblos es minimizar d(a) pues la distancia del puente es la misma para todos los casos
minimizemos d(a), para ello derivamos
d'(a)= ...
igualamos a cero
...
resolvemos la ecuación racional
...
tenemos como solución
a=0
por lo tanto a=0 y b=2
Los puntos son P(0,2) y Q(2,0)
-
Ronald Dominguez
el 22/3/17
Alguien me podria ayudar con el ejercicio 7? sobre todo con el inciso a no se como comprobar si es alabeada, gracias de antemano.Antonio
el 22/3/17Antonio
el 22/3/17no son paralelas ni coincidentes ya que sus vectores directores (1,2,3) y (2,-1,1) no son proporcionales
tampoco se cortan en un punto, pues de existir ese punto al calcularlo:
x = 5+λ = 2+2μ => λ - 2μ = -3
y = -4+2λ = 0-μ => 2λ + μ = 4
x = -2+3λ = 1+μ => 3λ - μ = 3
Con las dos primerasλ - 2μ = -3
2λ + μ = 4
Resolvemos el sistema de ecuaciones:
λ = 1
μ = 2
Sustituyendo en la tercera
3λ - μ = 3
3·1 - 2 = 1 ≠ 3
No existe punto de corte, no se cortan
-
D.dani
el 22/3/17
![\[ S_n = \frac{b}{n} \cdot 2 \left( \frac{b}{n} \right)^2 + \frac{b}{n} \cdot 2 \left( \frac{2b}{n} \right)^2 + \cdots + \frac{b}{n} \cdot 2 \left( \frac{(n-1)b}{n} \right)^2 + \frac{b}{n} \cdot 2 \left( \frac{bn}{n} \right)^2. \]](http://13997-presscdn-0-70.pagely.netdna-cdn.com/wp-content/ql-cache/quicklatex.com-f99d7b65bb006f31aa7c69d4da31fec7_l3.svg "Rendered by QuickLaTeX.com")
![\[ \sum_{i=1}^n i^2 = \frac{n^3}{3} + \frac{n^2}{2} + \frac{n}{6}, \]](http://13997-presscdn-0-70.pagely.netdna-cdn.com/wp-content/ql-cache/quicklatex.com-514d7726c4500406a41737e87bc8261d_l3.svg "Rendered by QuickLaTeX.com")
![\[ 1^2 + 2^2 + \cdots + (n-1)^2 < \frac{n^3}{3} < 1^2 + 2^2 + \cdots + n^2. \]](http://13997-presscdn-0-70.pagely.netdna-cdn.com/wp-content/ql-cache/quicklatex.com-a7e04f565f0f6d5510d358d95925eefe_l3.svg "Rendered by QuickLaTeX.com")
![\[ A = \frac{2b^3}{3}. \qquad \blacksquare \]](http://13997-presscdn-0-70.pagely.netdna-cdn.com/wp-content/ql-cache/quicklatex.com-6b1ea7298730e94a3e3fcf5bf6a08bb5_l3.svg "Rendered by QuickLaTeX.com")
