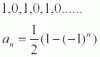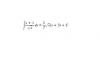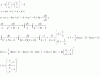-
Antonio Silvio Palmitano
el 17/2/17Debes corregir. Tienes el argumento de la integral:
f(x) = x3*(x5 - 2)2 = desarrollamos el binomio elevado al cuadrado
= x3*(x10 - 4x5 + 4) = distribuimos = x13 - 4x8 + 4x3.
Luego, pasamos a la integral del enunciado:
∫ (x3*(x5 - 2)2)*dx = sustituimos:
= ∫ (x13 - 4x8 + 4x3)*dx = separamos en términos:
= ∫ x13*dx - ∫ 4x8*dx + ∫ 4x3*dx = extraemos factores constantes en los dos últimos términos:
= ∫ x13*dx - 4*∫ x8*dx + 4*∫ x3*dx = resolvemos término a término:
= x14/14 - 4*x9/9 + 4*x4/4 + C = resolvemos coeficientes en los términos:
= (1/14)*x14 - (4/9)*x9 + x4 + C.
Espero haberte ayudado.
-
Hola David, me podrias ayudar con un video acerca de las tablas de verdad, no encuentro el video, asi que te agradeceria mucho si subes un video acerca de las tablas de verdad.
Ángel
el 18/2/17 -
Hola, tengo un problema de progresión aritmética de obtener el termino general an. He visto los vídeos que hay de este tema pero al aplicar la formula no me lo hace. La sucesión es la (1,0,1,0,1,0...) y quiero calcular el termino general.
-
Hallar la ecuacion de la recta tangente a la curva
C: xz-2z-3x+3=0
z^2-yz-4z+3y+4=0
en el punto to
Alguien que me ayude , gracias
Antonio Silvio Palmitano
el 17/2/17Vamos con dos formas para obtener un vector tangente a la curva, la primera empleando vectores normales a las superficies cuyas ecuaciones tienes en el enunciado, y la segunda por medio de una parametrización:
1°)
Tienes a la curva presentada como intersección de dos superficies, cuyas ecuaciones cartesianas implícitas son:
xz - 2z - 3x + 3 = 0, observa que es la ecuación de una superficie de nivel de la función cuya expresión es:
F(x,y,z) = xz - 2z - 3x + 3 = 0,
z2 - yz - 4z + 3y + 4 = 0, observa que es la ecuación de una superficie de nivel de la función cuya expresión es: G(x,y,z) = z2 - yz - 4z + 3y + 4 = 0,
observa que ambas funciones son diferenciables en R3, y que sus vectores gradientes tienen componentes:
∇F(x,y,z) = < z-3 , 0 , x-2 > = N1, que es el vector normal en cualquier punto de la superficie de nivel correspondiente,
∇G(x,y,z) = < 0 , -z+3 , 2z-y > = N2, que es el vector normal en cualquier punto de la superficie de nivel correspondiente,
luego, planteamos al vector tangente a la curva intersección entre ambas superficies como el producto vectorial de sus vectores normales:
u = N1 x N2 = < z-3 , 0 , x-2 > x < 0 , -z+3 , 2z-y > = < -(x-2)(-z+3) , -(z-3)((2z-y) , (z-3)(-z+3) >.
2°)
Hacemos pasajes de términos en ambas ecuaciones y quedan:
xz - 3x = 2z - 3, extraes factor común en el primer miembro y queda: x(z - 3) = 2z - 3, haces pasaje de factor como divisor y queda:
x = (2z - 3)/(z - 3) (1);
- yz + 3y = - z2 + 4z - 4, multiplicas en todos los términos por -1 y queda: yz - 3y = z2 - 4z + 4, factorizas y queda: y(z - 3) = (z - 2)2, haces pasaje de factor como divisor y queda:
y = (z - 2)2/(z - 3) (2).
Luego, planteamos: z = t, reemplazamos en las ecuaciones señaladas (1) (2), y tenemos las ecuaciones cartesianas paramétricas de la curva:
x = (2t - 3)/(t - 3)
y = (t - 2)2/(t - 3)
z = t,
con t ∈ R, t ≠ 3.
Luego, puedes plantear la función vectorial de posición:
r(t) = < (2t - 3)/(t - 3) , (t - 2)2/(t - 3) , t >, con t ∈ R, t ≠ 3;
y luego derivas con respecto a t, y tienes la expresión de un vector tangente a la curva en todos sus puntos, excepto los que tengan cota: z = t = 3.
Espero haberte ayudado.
-
Hola buenas noches. Estoy intentado resolver esta integral, pero el resultao no concuerda con el propocionado por el libro. Me podrian ayudar con los pasos a seguir para solucionarlo, para ver cual es mi falla? Mi resultado:
2√x³/3+ 2√x+c . Feliz noche
-
- Ayuda, necesito que me expliquéis de donde salio este uno, que el libro no lo explica y lo demás lo comprendo

Facu Imfeld
el 17/2/17Ese 1 resulta de un factor común realizado, tu tienes
5^x + 5^x.125
El factor repetido es 5^x, entonces puede sacarse como factor común
5^x.(1 + 125)
Escribe el 1 porque multiplicando por
el factor común, o sea 5^x . 1, te da como resultado el primer 5^x, luego escribe el 125 porque multiplicando el factor común por 125 te da 5^x.125, es decir, la expresión que tenías antes
-
David
el 20/2/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)