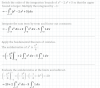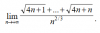-
Enrique Sánchez Sancho
el 16/2/17 -
Javier Laja Iglesias
el 16/2/17 -
Enrique Sánchez Sancho
el 16/2/17Integral entre 0 y x de tg t dt , me ha salido : -ln x dt + ln o dt ¿Está bien?
Fran Foce
el 16/2/17
Antonio Silvio Palmitano
el 16/2/17Planteamos la integral, por el momento indefinida:
∫ tant*dt = ∫ (sent/cost)*dt =
aplicamos la sustitución: w = cost, de donde tenemos: dw = - sent*dt, multiplicamos por -1 en ambos miembros y tenemos: - dw = sent*dt,
luego sustituimos y queda:
= ∫ (- dw)/w = - ∫ (1/w)*dw = - ln|w| + C.
Luego planteamos la integral definida del enunciado (indicamos con corchetes que aplicamos la Regla de Barrow):
0∫x tant*dt = [ - ln|w| ] = sustituimos = [ - ln|cost| ] = ( - ln|cosx| ) - (- ln|cos0| ) = - ln|cosx| + ln1 = - ln|cosx| + 0 = - ln|cosx|.
Espero haberte ayudado.
-
Sonia Ramis García
el 16/2/17
Hola!! ¿Puede alguien explicarme cómo se resuelve este ejercicio? con un poquito de explicación de por medio... ? miles de gracias. aprendo mucho con este foro.
-
Ingrid
el 16/2/17Me podrían ayudar a graficar las siguientes ecuaciones, por favor. Gracias.
-
Kainanteh Kainante
el 16/2/17El problema es el siguiente:
Encontrar el limite de limn->∞ n!/nn usando el teorema del emparedado (https://es.wikipedia.org/wiki/Teorema_del_emparedado), mi intento ha sido este:
En el supuesto 3 : n = 3 , n! = 3*2*1 = 6 , nn = 33 = 9 : por lo tanto puedo decir que n <= n! <= nn
Entonces para poder realizar el teorema del emparedado quedaria: n/nn <= n!/nn<=1
En limites : limn->∞ n/nn <= limn->∞ n!/nn <= lim n->∞ 1
El resultado: 0 <= limn->∞ n!/nn <= 1
El fallo evidentemente es que en vez de 0 tendría que dar 1, para así cumplir el teorema, creo que la solución seria cambiar al principio la n, por algo que fuera mas pequeño que n! y nn y diera 1, espero que alguien pueda ayudar.
-
Ángel Zhou Hu
el 16/2/17 -
Andres Montoro Menor
el 16/2/17Como encuentro el angulo y punto de intersección de estas rectas?
Antonio Silvio Palmitano
el 16/2/17Tienes las ecuaciones cartesianas paramétricas de la recta r, que pueden escribirse:
x = 1 + 1t
y = - 2 + 1t
z = 2 + 2t
con t ∈ R,
de donde tienes que su vector director tiene componentes: u = <1,1,2>, cuyo módulo es: ||u|| = √(6).
Tienes las ecuaciones cartesianas continuas (o simétricas) de la recta s, que pueden escribirse:
(x - 0)/1 = (y + 3)/(-1) = (z - 0)/1,
de donde tienes que su vector director tiene componentes: v = <1,-1,1>, cuyo módulo es: ||v|| = √(3).
Luego, calculamos el producto escalar entre los vectores directores:
u • v = <1,1,2> • <1,-1,1> = 1*1 + 1*(-1) + 2*1 = 1 - 1 + 2 = 2.
Luego, planteamos la expresión del producto escalar entre los vectores directores, en función de sus módulos y del ángulo determinado por ellos:
u • v = ||u||*||v||*cosα, reemplazamos valores ya calculados y queda:
2 = √(6)*√(3)*cosα, resolvemos el producto de raíces y queda:
2 = √(18)*cosα, hacemos pasaje de factor como divisor y queda:
2/√(18) = cosα, componemos con la función inversa del coseno y queda:
α ≅ 61,87°.
Espero haberte ayudado.
-
Mile
el 16/2/17Como se termina de hacer esta integral? LO QUE HICE NO SE SI ESTA BIEN!
Antonio Silvio Palmitano
el 16/2/17Has planteado bien el método de integración por partes, pero debes corregir su resolución y la evaluación con la Regla de Barrow en tu última lí
Tienes la integral, por el momento indefinida:
∫ x*lnx*dx = lnx*(x2/2) - ∫ (x2/2)*(1/x)*dx = lnx*(x2/2) - (1/2)* ∫ x*dx = lnx*(x2/2) - (1/2)*(x2/2) + C = lnx*(x2/2) - x2/4 + C.
Luego evaluamos (indicamos con corchetes que aplicamos la Regla de Barrow):
1∫2 x*lnx*dx = [ lnx*(x2/2) - x2/4 ] = evaluamos = (ln2*2 - 1) - (ln1*1/2 - 1/4) = resolvemos términos y distribuimos agrupamientos = 2*ln2 - 1 - 0 + 1/4 = 2*ln2 - 3/4.
Espero haberte ayudado.
