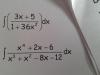-
Hola.
Disculpen la molestia pero seria posible que me colaboren con el siguiente problema de estadística:
De un grupo de 140 obreros que laboran en una fábrica, 53 de ellos son menores de 25 años y el resto son mayores de 25 años. Se sabe que el total de obreros en promedio fabrican 1250 unidades del producto A, y además, que los trabajadores mayores de 25 años producen en promedio el doble de los otros ¿cuál es la producción promedio de cada grupo?
De antemano muchas gracias.
Antonio Silvio Palmitano
el 16/2/17Tenemos una población de 140 obreros dividida en dos clases: 53 jóvenes y 87 mayores.
Llamamos N a la cantidad total de artículos producidos.
Tenemos, a partir del promedio general del enunciado: N/140 = 1250, de donde tenemos: N = 140*1250 = 175000.
Llamamos:
N1 a la cantidad de artículos producido por el grupo de jóvenes, y su promedio: p1 = N1/53, de donde despejamos: 53*p1 = N1.
Llamamos:
N2 a la cantidad de artículos producido por el grupo de mayores, y su promedio: p2 = N2/87, de donde despejamos: 87*p2 = N2..
Luego planteamos el sistema de ecuaciones:
N1 + N2 = N
2*p1 = p2
Sustituimos el valor de N y las expresiones de N1 y N2 y queda:
53*p1 + 87*p2 = 175000
2*p1 = p2 (1).
Sustituimos la expresión remarcada en la primera ecuación y queda:
53*p1 + 174*p1 = 175000, reducimos términos semejantes y queda:
227*p1 = 175000, hacemos pasaje de factor como divisor y queda:
p1 ≅ 770,9, de donde tenemos: N1 = 53*770,9 ≅ 40859.
Reemplazamos en la ecuación señalada (1) y queda:
p2 ≅ 1541,8, de donde tenemos: N2 = 87*1541,8 ≅ 134141.
Por lo tanto, concluimos:
el grupo de jóvenes produce aproximadamente 40859 unidades, y que su promedio es 771 unidades por obrero, y
el grupo de mayores produce aproximadamente 134141 unidades, y que su promedio es 1542 unidades por obrero.
Espero haberte ayudado.
-
La estatua de la libertad de nueva york mide 30.6 m de cabeza a pies. Si con esta se reprodujo una persona de una medida de 170 cm, que escala usaron para su construcción?
Ángel
el 16/2/17Pasamos las dos medidas a centímetros o metros, nosotros elegiremos por ejemplo, los centímetros
Medida de la persona: 170 cm
Medida de la estatua: 3060 cm
3060/170= 306/17= (18x17)/17= 18
SOLUCIÓN CON TU ENUNCIADO: Usaron la escala de reducción 1:18 para "reproducir" una persona de una medida de 170 cm a partir de la estatua de New York (tenía cara de edificio el pobre:D)
--> ENUNCIADO MÁS COHERENTE: "hallar la escala que se usó para hacer la estatua de la libertad de 30.6 m, si se construyó reproduciendo a una persona de 170 cm"
Usaron la escala de ampliación 18:1 para reproducir la estatua de New York partiendo de una persona
-
Antonius Benedictus
el 16/2/17AnDres Navarrete
el 16/2/17 -
Antonio Silvio Palmitano
el 16/2/17Primero, observa que tienes una fracción algebraica en el argumento de la integral y, como el polinomio numerador (P(x)) tiene grado 4, que es mayor que el grado del denominador (Q(x)), efectúa la división con el algoritmo, y tendrás que el cociente es: C(x) = x - 1, y el resto es: R(x) = 9x2 + 6x - 6.
Luego, la fracciópn puede escribirse:
P(x)/Q(x) = C(x) + R(x)/Q(x) = x - 1 + (9x2 + 6x - 6)/(x3 + x2 - 8x - 12).
Luego, ya puedes integrar directamente en los dos primeros términos, y para el tercero planteamos el método de las fracciones parciales, observa que -2 y 3 son raíces del denominador, por lo que planteamos la Regla de Ruffini: en forma sucesiva (comenzamos con la raíz 3, y luego seguimos con la raíz -2)
1 1 -8 -12
3 3 12 12
1 4 4 0
-2 -2 -4
1 2 0
-2 -2
1 0
luego, tenemos que el polinomio denominador queda factorizado: Q(x) = (x - 3)(x + 2)2.
Luego, planteamos el método de las fracciones parciales para el término fraccionario del cociente (lo iniciamos, queda para que concluyas la tarea, y el resto del ejercicio):
(9x2 + 6x - 6)/(x3 + x2 - 8x - 12)(x3 + x2 - 8x - 12) = (9x2 + 6x - 6)/(x - 3)(x + 2)2 = planteamos las fracciones parciales =
= a/(x - 3) + b/(x + 2) + c/(x + 2)2 = (1) extraemos denominador común:
= ( a(x + 2)2 + b(x + 2)(x - 3) + c(x - 3) )/(x - 3)(x + 2)2
por igualdad entre fracciones algebraicas con denominadores iguales, planteamos la igualdad entre los numeradores que hemos remarcado:
a(x + 2)2 + b(x + 2)(x - 3) + c(x - 3) = 9x2 + 6x - 6,
luego evaluamos para tres valores distintos de x, por ejemplo: -2, 3 y 0, y queda el sistema de tres ecuaciones con tres incógnitas:
- 5c = 18
25a = 39
4a - 6b - 3c = - 6
luego, queda para que resuelvas el sistema, y reemplaces los valores de los coeficientes en la expresión señalada (1), y ya tienes el tercer término, por lo que puedes pasar a resolver la integral del enunciado.
Haz el intento, y si te es preciso, no dudes en volver a consultar.
Espero haberte ayudado.
-
Hola buenas unicoos. Vereis mi duda es sobre mi resolución de una derivada: Dada f(x) = x+1/x-3 halla f´(1)
Yo he hecho:
f´(1) = limh->0 f(x0+h) - f(x0) / h = f(1) - f(1) / 0 = 0/0
limh->0 f(x0+h) - f(x0) / h Ξ limx->1 f(x) - f(x0) / x - x0
limx->1 f(x) - f(x0) / x - x0 = limx->1 (3x-2 / 2x-6) / x - x0 = 1/0 = ∞
¿Sería correcto el resultado y el procedimiento? Gracias
Antonio Silvio Palmitano
el 16/2/17Tenemos la función cuya expresión es: f(x) = (x + 1)/(x - 3), luego planteamos la definición para la derivada de la función en x = 1:
f ' (1) = Lím(h→0) ( f(1+h) - f(1) )/ h = Lím(h→0) (1/h)*( f(1+h) - f(1) ) (A).
Luego calculamos los términos del numerador por separado:
f(1) = (1 + 1)/(1 - 3) = 2/(-2) = - 1,
f(1+h) = (1 + h + 1)/(1 + h - 3) = (h + 2)/(h - 2);
luego planteamos:
f(1+h) - f(1) = (h + 2)/(h - 2) - (- 1) = (h + 2)/(h - 2) + 1 = extraemos denominador común:
= (h + 2 + h - 2)/(h -2) = 2*h/(h - 2).
Luego pasamos al cálculo de la derivada, reemplazamos en la expresión señalada (A) y queda:
f ' (1) = Lím(h→0) (1/h)*2*h/(h - 2) = simplificamos factores = Lím(h→0) 2/(h - 2) = evaluamos = 2/(0 - 2) = 2/(- 2) = - 1.
Espero haberte ayudado.