-
Antonio Silvio Palmitano
el 1/2/171)
Mostramos los datos en una tabla de valores:
q p
10 90
20 30
Luego, calculamos la pendiente: m = (30 - 90)/(20- 10) = - 60/10 = - 6 (en $/par).
Luego, planteamos la ecuación (observa que empleamos los datos de la primera línea y la pendiente):
p - 90 = - 6*(q - 10), distribuimos en el segundo miembro y queda:
p - 90 = - 6*q + 60, hacemos pasaje de término numérico y queda:
p = - 6*q + 150, por lo que concluimos que la opción a es la respuesta correcta.
2)
Planteamos la igualdad entre precios de oferta y de demanda, que es la condición de equilibrio:
4q + 15 = - q + 60, hacemos pasajes de términos y queda:
5q = 45, hacemos pasaje de factor como divisor y queda:
q = 9 (en miles de unidades), que es la cantidad de equilibrio;
luego reemplazamos en las ecuaciones (observa que en ambas obtenemos el mismo resultado).
p = 4*9 + 15, resolvemos el primer término numérico y queda:
p = 36 + 15, resolvemos y queda:
p = 51, que es el precio de equilibrio.
Luego, concluimos que la opción d es la respuesta correcta.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 1/2/171)
Tienes las coordenadas de los puntos A(2,1) y B(-15,5) que pertenecen a la recta.
Luego, calculamos la pendiente: m = (5 - 1)/(- 15 - 2) = 4/(-17) = - 4/17;
luego planteamos su ecuación cartesiana (observa que empleamos las coordenadas del punto A):
y - 1 = - (4/17)*(x - 2), distribuimos en el segundo miembro y queda:
y - 1 = - (4/17)*x + 8/17, hacemos pasaje de término numérico y queda:
y = - (4/17)*x + 8/17 + 1, reducimos términos numéricos y queda:
y = - (4/17)*x + 25/17, que es la ecuación cartesiana explícita de la recta.
2)
Ordenamos los datos del enunciado en en una tabla de valores e indicamos con x a la cantidad de sillas (en cientos de unidades), y con c al costo (en miles de $).
x c
3,5 125
4,5 145
Luego, suponemos que las variables x y c se relacionan linealmente, por lo que plantamos:
pendiente: m = (145 - 125)/(4,5 - 3,5) = 20/1 = 20 (en $/cientos de unidades);
luego planteamos la ecuación (observa que empleamos los datos de la primera línea):
c - 125 = 20*(x - 3,5), distribuimos en el segundo miembro y queda:
c - 125 = 20*x - 70, hacemos pasaje de término, reducimos términos numéricos y queda:
c = 20*x + 55 (en $).
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 1/2/17Observa que el punto de intersección entre las diagonales del cuadrado tiene coordenadas: M(-4,3),
y observa que el centro de simetría tiene coordenadas: P(-1,2);
luego planteamos que el simétrico del punto M con respecto al centro P tiene coordenadas: N(x,y).
Luego, recuerda que el centro de simetría P es el punto medio entre los puntos M y N, por lo que tenemos (observa que promediamos las coordenadas de los puntos M y N):
P( (-4+x)/2 , (3+y)/2 ),
luego, tenemos las ecuaciones:
(- 4 + x)/2 = - 1
(3 +y)/2 = 2
multiplicamos por 2 en ambos miembros de ambas ecuaciones y queda:
- 4 + x = - 2, de donde despejamos: x = 2
3 + y = 4, de donde despejamos: y = 1
Luego, concluimos que el punto simétrico del punto M con respecto al centro de simetría P tiene coordenadas: N(2,1).
Puedes corroborar en el gráfico que la solución es válida.
Espero haberte ayudado.
-
¿Estaría bien el apartado b? Se trata de sacar la inversa por Gauss, en mi libro de texto viene como solución otra cosa y no sé
Gabriel
el 31/1/17Antonio Silvio Palmitano
el 1/2/17Recuerda que las operaciones elementales son:
a) Multiplicar a una fila por un número distinto de cero.
b) A una fila sumarle (o restarle) un múltiplo de otra fila.
c) Permutar filas.
Es importante que observes que las operaciones son entre filas (no podemos sumarle o restarle un número fijo a una fila).
1)
Planteamos la doble matriz:
1 1 1 0
0 1 0 1
A la primera fila le restas la segunda fila y queda:
1 0 1 -1
0 1 0 1
Luego, tienes que la matriz inversa de A tiene los elementos que hemos remarcado.
2)
Planteamos la doble matriz:
1 2 1 0
3 4 0 1
A la segunda fila le restas el triple de la primera fila y queda:
1 2 1 0
0 -2 -3 1
A la primera fila se sumas la segunda fila y queda:
1 0 -2 1
0 -2 -3 1
A la segunda fila la multiplicas por -1/2 y queda:
1 0 -2 1
0 1 3/2 -1/2
Luego, tienes que la matriz inversa de B tiene los elementos que hemos remarcado.
Espero haberte ayudado.
-
Ayuda por favor Antonio Benito. Paso a paso. Gracias de antemano. Un saludo.
Resuelve:
a) x2-x-6<0
b) -x2+3x-2≤0
c) -x2+4x>0
Antonius Benedictus
el 31/1/17Antonius Benedictus
el 31/1/17María
el 31/1/17María
el 31/1/17María
el 1/2/17 -
Antonio Silvio Palmitano
el 1/2/17a)
Observa que debes agregar una línea: aplicas la regla de los signos y queda: x = 7/3.
b)
Observa que tu segunda línea (que has planteado correctamente) quedó:
7x2 - 2x2 - 5x2 = - 2 + 10, resuelves en cada miembro por separado y queda:
0x2 = 8, observa que el primer miembro es nulo y queda:
0 = 8, que es una identidad falsa, por lo que concluimos que la ecuación no tiene solución.
c)
Observa que debes agregar una línea: multiplicas por - 1 en ambos miembros y queda: x = 8.
d)
Tienes la ecuación:
12x2 + 4 = 2*(6x2 + x + 7), distribuyes en el segundo miembro y queda:
12x2 + 4 = 12x2 + 2x + 14, haces pasajes de términos y queda:
12x2 - 12x2 - 2x = 14 - 4, cancelas términos opuestos en el primer miembro, resuelves el segundo miembro y queda:
- 2x = 10, haces pasaje de factor como divisor y queda:
x = 10/(-2), resuelves el segundo miembro y queda:
x = - 5.
Espero haberte ayudado.
-
Antonius Benedictus
el 31/1/17






































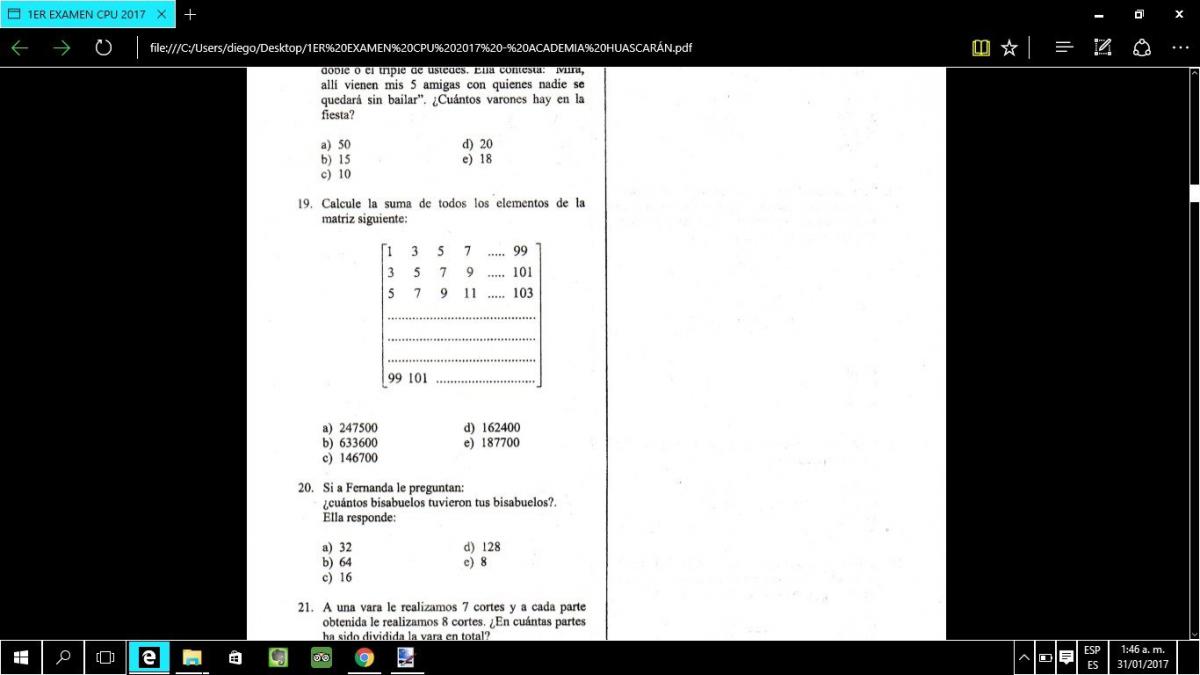 si me ayudan con el 19 y el 20 por favor
si me ayudan con el 19 y el 20 por favor


