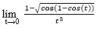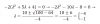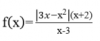-
Fredy
el 30/1/17Hola Ayudarme con este ejercicio
Antonio Silvio Palmitano
el 31/1/17Planteamos:
Llamamos x a la cantidad de lámparas vendidas (observa que x toma valores naturales).
a) Ingreso = precio de venta * cantidad de lámparas vendidas, reemplazamos y queda: I(x) = 90*x (en Soles).
b) Costo total = costo fijo + costo de fabricación por unidad * cantidad de lámparas producidas, reemplazamos y queda: C(x) = 8000 + 40*x (en Soles).
c) Utilidad = Ingreso - Costo total, reemplazamos y queda: U(x) = 90*x - (8000 + 40*x) = 90*x - 8000 - 40*x, reducimos términos semejantes y queda: U(x) = 50*x - 8000 (en Soles)..
La cantidad mínima de lámparas a producir para no tener pérdida corresponde a la utilidad nula, por lo que planteamos:
U(x) = 0, sustituimos y queda:
50*x - 8000 = 0, hacemos pasaje de término y queda:
50*x = 8000, hacemos pasaje de factor como divisor y queda:
x = 160, y observa que para este valor tenemos:
I(160) = 90*160 = 14400 Soles;
C(160) = 8000 + 40*160 = 8000 + 6400 = 14400 Soles;
U(160) = 50*160 - 8000 = 8000 - 8000 = 0.
Queda para que hagas los gráficos, y observa que las tres gráficas son rectas.
Espero haberte ayudado.
-
Juanjo
el 30/1/17[URGENTE] - Algebra (Truco para ahorrar tiempo)
Tengo calculado ya la base y la dimensión del KER de una aplicación, la base de la im(f), ¿podrían ser vectores de la matriz de f?
ejemplo: f:R3→R4 f(x,y.z)=(x+2y−z,−x+y+2z,3y+z,3x−5z).
Matriz asociada:
( 1 2 -1)
( -1 1 2)
(0 3 2 )
(3 0 -5)
dim ker(f) = 1
R3 = dim ker(f) + dim im(f)
im(f) = 2
¿podemos coger como base de im(f) <(1,-1,0,3),(2,1,3,0)> ? Siempre y cuando dichos vectores sean linealmente independientes.
-
Marino Alfonso Redondo
el 30/1/17 -
antonella
el 30/1/17hola unicoos!! ayuda!!! como resuelvo ese ejercicio?? graciaaas!!! no entiendo lo que esta entre llaves y tampoco se como resolver los limites!
Antonio Silvio Palmitano
el 31/1/17Observa que tienes una función cuya expresión tiene tres trozos, cuyos puntos de corte son x = 2 y x = 5, y observa que la función no está definida en x = 5.
a) Observa que x = 0 corresponde al primer trozo, por lo que planteamos:
Lím(x→0+) f(x) = Lím(x→0+) (3 - x ) = 3.
b) Observa que x = 0 corresponde al primer trozo, por lo que planteamos:
Lím(x→0-) f(x) = Lím(x→0-) (3 - x ) = 3.
c) Como los dos límites laterales coinciden, tenemos: Lím(x→0) f(x) = Lím(x→0) (3 - x ) = 3.
d) Observa que x = 2 es un punto de corte entre trozos, por lo que planteamos:
Lím(x→2+) f(x) = Lím(x→2+) (x) = 2
f) Observa que x = 2 es un punto de corte entre trozos, por lo que planteamos:
Lím(x→2-) f(x) = Lím(x→2-) (3 - x) = 1.
e) Como los límites laterales no coinciden, tenemos: Lím(x→2) f(x) no existe (pero observa que x = 2 pertenece al dominio de la función).
h) Observa que x 0 5 es un punto de corte entre trozos, por lo que planteamos:
Lím(x→5+) f(x) = Lím(x→5+) (x + 1) = 6.
i) Observa que x 0 5 es un punto de corte entre trozos, por lo que planteamos:
Lím(x→5+) f(x) = Lím(x→5+) (x) = 5.
g) Como los límites laterales no coinciden, tenemos: Lím(x→5) f(x) no existe (pero observa que x = 5 no pertenece al dominio de la función).
Espero haberte ayudado.
-
Maite Caro
el 30/1/17 -
Mario Peña
el 30/1/17 -
Rubén
el 30/1/17
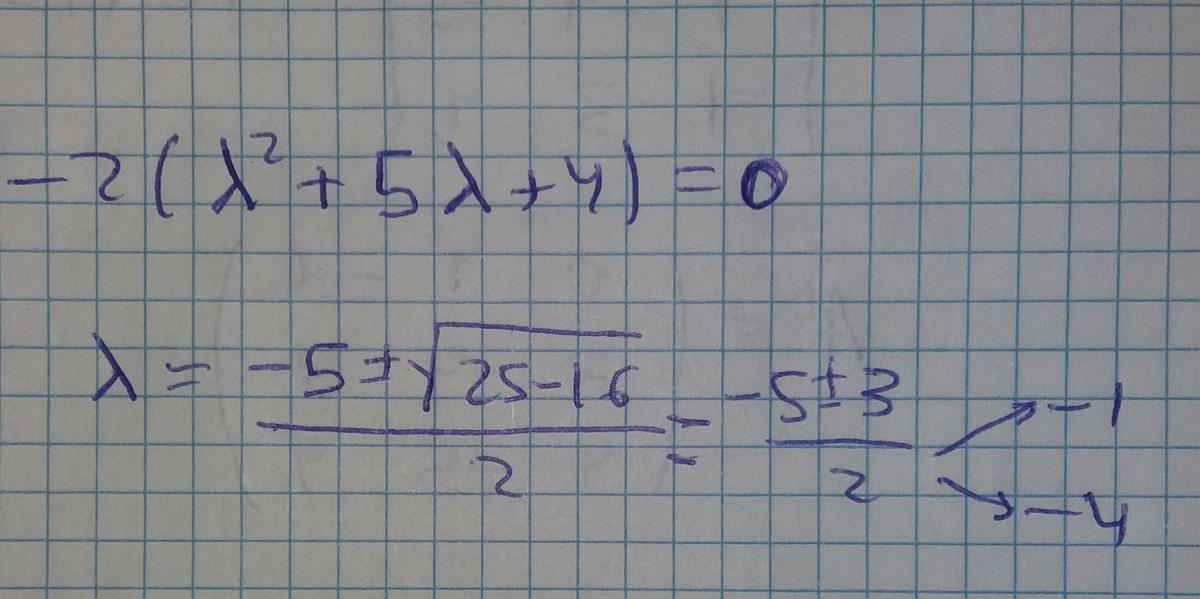¿Por qué no se multiplica el -2 por lo que está entre paréntesis para resolver la ecuación? La he resuelto multiplicandolo y no me salía lo mismo.Damián
el 30/1/17 -
Mario Peña
el 30/1/17 -
Pilar
el 30/1/17
Cómo podría hacer la integral esta por partes ? Damián
el 30/1/17 -
Jose
el 30/1/17
Hola unicoos, intente hacer este ejercicio pero me dieron numero demasiado grandes lo cual supuse que lo qe estaba haciendo estaba muy mal, lo que hice fue encontrar esa f(x), haciendo la multiplicacion que dice el enunciado y me quedo
f(x)= x3-5x2-9x+45 / (x+4) luego la derivada 2x3+7x2-40x-81/ (x+4)2
