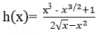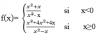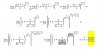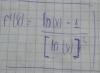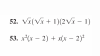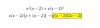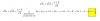-
Buen día!!
Podrían ayudarme con el procedimiento de este problema, muchas gracias!!
Halle las asíntotas verticales, horizontales y oblicuas de la función:


Antonio Silvio Palmitano
el 30/1/17Comencemos por establecer el dominio de la función:
observa que x debe ser estrictamente positivo, porque si es igual a cero se anula el denominador, y si x es negativo se indetermina su primer término. Luego planteamos:
2√(x) - x2 ≠ 0, escribimos la raíz cuadrada como potencia fraccionaria:
2x1/2 - x2 ≠ 0, extraemos factor común:
x1/2 *(2 - x3/2) ≠ 0, luego, por anulación de un producto tenemos dos opciones:
a) x1/2 ≠ 0, de donde despejamos: x ≠ 0;
b) 2 - x3/2 ≠ 0, hacemos pasaje de término: 2 = x3/2 , luego despejamos: x ≠ 22/3= ∛(4).
Luego, el dominio de la función expresado como intervalo queda: D = (0,22/3) u (22/3,+∞).
Luego, pasamos al estudio de las asíntotas:
1) Posibles Asíntotas Verticales: x = 0, x = 22/3.
1a) Lím(x→0+) f(x) = ∞ (observa que el numerador tiende a 1 y el denominador tiende a cero desde valores positivos),
por lo que tenemos que la gráfica de la función presenta asíntota vertical, cuya ecuación es: x = 0;
1b) Lím(x→∛(4)) f(x) = ∞ (observa que el numerador tiende a 3 y el denominador tiende a cero),
por lo que tenemos que la gráfica de la función presenta asíntota vertical, cuya ecuación es: x = ∛(4).
2) Posibles Asíntotas Horizontales:
Lím(x→+∞) f(x) = -∞ (observa que el mayor exponente en el numerador es 3 y el signo de su término es positivo, y que el mayor exponente en el denominador es 2 y el signo de su término es negativo, por lo que tienes que el numerador es de mayor orden de magnitud que el denominador),
por lo que tenemos que la gráfica de la función no presenta asíntota horizontal.
3) Posibles Asíntotas Oblicuas:
3a) estudiamos el límite para x tendiendo a infinito de la pendiente:
Lím(x→+∞) f(x)/x = dividimos por x en todos los términos del numerador:
= Lím(x→+∞) (x2 - x1/2 + 1/x)/(2√(x) - x2) =
dividimos por x2 en todos los términos de la expresión para determinar órdenes de magnitud:
= Lím(x→+∞) (1 - 1/x3/2 + 1/x3)/(2/x3/2 - 1) = 1/(-1) = - 1 = m;
3b) estudiamos el límite para x tendiendo a infinito para determinar el valor de la ordenada al origen:
Lím(x→+∞) (f(x) - mx) = reemplazamos:
= Lím(x→+∞) ( (x3 - x3/2 + 1)/(2√(x) - x2) + x ) = extraemos denominador común:
= Lím(x→+∞) ( x3 - x3/2 + 1 + 2x3/2 - x3 )/(2√(x) - x2) = reducimos términos semejantes en el numerador:
= Lím(x→+∞) ( x3/2 + 1 )/(2√(x) - x2) = dividimos en todos los términos de la expresión por x2:
= Lím(x→+∞) ( 1/x1/2 + 1/x2 )/(2/x3/2 - 1) = 0/(-1) = 0 = b.
Luego, planteamos la ecuación cartesiana explícita de la asíntota oblicua (y = mx + b) y queda: y = - x.
Espero haberte ayudado.
-
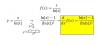
Buenos días. En un ejercicio tengo que hallar la ecuacion de la recta tangente a la curva descrita por
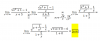
 en el punto de abscisa x=1 y ordenada positiva. Obtengo el punto (1,1), calculo la derivada implicita que es
en el punto de abscisa x=1 y ordenada positiva. Obtengo el punto (1,1), calculo la derivada implicita que es 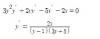 pero al sustituir los valores en el punto (1,1) el denominador me da 0. ¿Esta bien, podría seguir de alguna forma o no puedo resolverlo?
pero al sustituir los valores en el punto (1,1) el denominador me da 0. ¿Esta bien, podría seguir de alguna forma o no puedo resolverlo?Muchas gracias por su atencion.
-
hola, me podrian decir porque los resultados no concuerdan con los de las opciones? yo hice esto: (3,-2,-1).(a,b,c) = 3a-2b-c=0 el vector (1,1,1) verifica luedo (x,y,z)= (1,1,1) +(1,1,1)β, pasandolas a interseccion de planos quedaria asi x-1-y+1=0 y y-1-z+1=0 quedando como resultado final { x-y=0 y y-z=0 quisiera saber que hago mal , no me importa tanto el resultado sino saber que esta mal.

-


Antonio Silvio Palmitano
el 30/1/17Tienes la ecuación:
(t - 4)2 = (t + 4)2 + 32, desarrollas los binomios elevados al cuadrado y queda:
t2 - 8t + 16 = t2 + 8t + 16 + 32, haces pasajes de términos (observa que tienes cancelaciones de términos opuestos) y queda:
- 16t = 32, haces pasaje de factor como divisor y queda:
t = - 2.
Espero haberte ayudado.