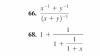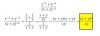-
Antonio Silvio Palmitano
el 30/1/17Vamos con el ejercicio 68.
Primero, estudiemos el denominador de la primera fracción:
1 + 1/(1+x) = extraemos denominador común = (1 + x + 1)/(1+x) = (2+x)/(1+x).
Luego, estudiemos la primera fracción:
1 / ( 1 + 1/(1+x) ) = sustituimos = 1 / ( (2+x)/(1+x) ) = resolvemos la división entre expresiones fraccionarias = (1 + x)/(2+x).
Por último, pasamos a la expresión del enunciado:
1 + ( 1 / ( 1 + 1/(1+x) ) ) = sustituimos = 1 + (1 + x)/(2+x) = extraemos denominador común =(2 + x + 1 + x)/(2+x) = (3 + x)/(2 + x).
Espero haberte ayudado.
-
- Hola mucho gusto esperaba que me ayudaran con este problema por favor y gracias
- 1+ log3x/1+ logx3=1/3 ; x> 0 o x=1
Axel Morales Piñón.
el 30/1/17Antonio Silvio Palmitano
el 30/1/17Tienes la ecuación logarítmica:
(1 + log3x)/(1 + logx3) = 1/3
Observa que el denominador no puede ser nulo, por lo que planteamos:
1 + logx3 ≠ 0, hacemos pasaje de término y queda:
logx3 ≠ - 1, componemos con la función inversa del logaritmo en base x en ambos miembros y queda:
3 ≠ x- 1, expresamos el segundo miembro en forma fraccionaria y queda:
3 ≠ 1/x, hacemos pasajes de divisor y de factor y queda:
x ≠ 1/3.
Luego, en la ecuación del enunciado hacemos pasajes de divisores como factores y queda:3*(1 + log3x) = 1*(1 + logx3), distribuimos en ambos miembros y queda:
3 + 3*log3x = 1 + logx3, hacemos pasaje de término numérico y queda:
2 + 3*log3x = logx3, aplicamos la fórmula de cambio de base en ambas expresiones logarítmicas (cambiamos a base decimal) y queda:
2 + logx/log3 = log3/logx, extraemos denominador común en el primer miembro y queda:
(2*log3 + logx)/log3 = log3/logx, hacemos pasajes de divisores como factores y queda:
(2*log3 + logx)*logx = (log3)2, distribuimos en el primer miembro y queda:
2*log3*logx + (logx)2 = (log3)2, hacemos pasaje de término, ordenamos términos y queda:
(logx)2 + 2*log3*logx - (log3)2 = 0, aplicamos la sustitución (cambio de incógnita): w = logx (observa que 10w = x) y queda:
w2 + 2*log3*w - (log3)2 = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:
a) w = - log3 + √(2)*log3 = (- 1 + √(2)*log3 ≅ 0,1976, que corresponde a: x = 10(- 1 + √(2)*log3 ≅ 1,5763;
b) w = - log3 - √(2)*log3 = (- 1 - √(2)*log3 ≅ - 1,1519, que corresponde a: x = 10(- 1 - √(2)*log3 ≅ 0,0705.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 30/1/17Puedes plantear el algoritmo de multiplicación
3333......333 (doscientas cifras
* 12
--------------------------
6666.....666 (doscientas cifras)
33333.....33 (doscientas una cifras, recuerda que estamos multiplicando desde las decenas en adelante)
--------------------------
39999....996 (doscientas una cifras, la primera es 3, la última es 6, y las ciento noventa y nueve intermedias son 9)
Luego, la suma total de cifras queda:
S = 3 + 199*9 + 6 = 3 + 1791 + 6 = 1800.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 30/1/17Está correcto, pero observa que podrías haber ahorrado pasos (transcribimos tu primera línea):
tan(2α) = sen(2α)/cos(2α) = 2*senα*cosα / (cos2α - sen2α) =
ahora puedes dividir en el numerador y en el denominador por cos2α, y observa que en el denominador puedes distribuir, luego queda:
= (2*senα*cosα/cos2α) / (cos2α/cos2α - sen2α/cos2α) =
luego simplificas factores y divisores y queda:
= (2*senα/cosα) / ( 1 - (senα/cosα)2 ) =
luego aplicamos la identidad para la tangente y queda:
= 2*tanα/(1 - tan2α).
Espero haberte ayudado.
-
hay algun video donde explique factorizar polinomios con metodo de rufinni? muchas gracias!
Axel Morales Piñón.
el 30/1/17