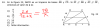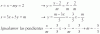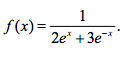-
Bet
el 30/1/17 -
Bet
el 30/1/17 -
Marino Alfonso Redondo
el 30/1/17
Buenas en esta funcion me piden calcular las primitivas al respecto, me podrian echar una mano, que yo fui de mates de letras y estoy pasandolo un poquillo mal con los ejercicios
-
Enrique Sánchez Sancho
el 30/1/17Calcula la inducción magnética en el centro de una espira de 12 cm de radio , por la que circula una corriente de 5,0 A de Intensidad.
- Compara este valor con el campo creado por un hilo indefinido, por el que circula la misma intensidad de corriente a una distancia de 12 cm , y comenta cómo influye la forma del conductor en el módulo del campo. El problema es que me ha salido 8,3 * 10-6 Teslas pero en el libro pon e ese resultado en Bhilo = 8,3 * 10-6 T cosa que no me cuadra mucho. Entonces el resultado de B espira no sé cómo sacarlo.
-
Alejandro Expósito
el 30/1/17(3/x−2)+(2x−1/x−1)
Ayuda??????
Antonio Silvio Palmitano
el 30/1/17Si lo que necesitas es sumar las expresiones algebraicas fraccionarias, ahí vamos:
3/(x+2) + (2x-1)/(x-1) = extraemos como mínimo común denominador al producto de los denominadores y queda
= ( 3(x-1) + (2x-1)(x+2) ) / (x+2)(x-1) = distribuimos en el numerador y queda:
= (3x - 3 + 2x2 + 4x - x - 2) / (x+2)(x-1) = reducimos términos semejantes y ordenamos en el numerador y queda
= (2x2 + 6x - 5) / (x+2)(x-1).
Observa que el numerador es un polinomio cuadrático cuyas raíces son: (-6-√(76))/4 y (-6+√(76))/4, por lo que al factorizarlo (puedes hacerlo si te resulta útil) no tiene factores comunes con el denominador, por lo que la expresión no es simplificable.
Espero haberte ayudado.
-
Desconocido
el 30/1/17
Estoy liado con un ejercicio de programación lineal, no se bien como plantear la función objetivo
Se tienen 1000kg de manzana, 600kg de ciruelas y 800kg de melocotones. Se venden a 0.4€/kg, 0.6€/kg y 0.8€/kg respectivamente.
Se quieren vender botes de mermelada y éstas son las opciones:
Mermeladas de un solo sabor.
Mermeladas de dos sabores: solo se puede de manzana con ciruela y manzana con melocotón (las de dos sabores tienen mitad y mitad de cantidad de cada fruta).
Por kg de fruta de consigue un kg de mermelada. Las de un sabor se venden a 2€, las de dos sabores a 2.5€.
Teniendo en cuenta que hay pedido mínimo de 175kg de mermelada de manzana, 160kg de mermelada de ciruela y 150kg de melocotón.
Entonces para plantear la función objetivo he llamado X1 a la cantidad de manzana, X2 a la de ciruela y X3 a la de melocotón y he planteado lo siguente:
F = 2*X1 + 2*X2 + 2*X3 + 2(0.5*X1 + 0.5*X2) + 2(0.5*X1 + 0.5*X3) - 0.4*X1 - 0.6X2 - 0.8X3 = 4.1*X1 + 2.65*X2 + 2.45*X3
X1, X2, X3 >= 0
175<=X1<=1000
160<=X2<=600
150<=X3<=800
Tengo bastantes dudas con la función objetivo.
-
Jordi García
el 30/1/17Hola UNICOOS,
¿Podéis ayudarme en este ejercicio?
Ej:
a) Escribir en forma binómica el complejo z = (2 + a·i) / (1 - i)
b) Hallar a para que z sea un imaginario puro.
El a me ha dado (√(4 + a2)cotg a/2 ) / (√2315º)
El b no tengo ni idea de cómo hacerlo.
Gracias.
Antonio Silvio Palmitano
el 30/1/17a) Multiplicamos al numeraodr y al denominador por el conjugado del denominador y queda:
z = (2 + ai)(1 + i) / (1 - i)(1 + i), distribuimos en el numerador y en el denominador y queda:
z = (2 - 2i + ai + ai2) / (1 + i - i - i2), resolvemos los cuadrados de i, cancelamos términos opuestos y queda
z = ( 2 - 2i + ai - a)/2, agrupamos términos reales e imaginarios, distribuimos el denominador y queda:
z = (2 - a)/2 + (- 2 + a)i/2.
b) Si z es un número complejo imaginario puro, planteamos que su parte real debe ser igual a cero:
(2 - a)/2 = 0, hacemos pasaje de divisor como factor y queda
2 - a = 0, hacemos pasaje de término y queda:
2 = a.
Espero haberte ayudado.
-
adrian
el 30/1/17 -
Gianluca
el 30/1/17
