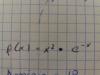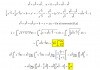-
Y si el limite cuandi tienede a infinito de x^2 por e^-x = indeterminación cero por infinito al transformarlo en una de infinito partido infinito porque se transforma así: x^2/e^x y no (e^2/(1/e^-x))?
-
TENGO UNA DUDA EN ESTE EJERCICIO DE INTERES SIMPLE, NO SÉ SI EL TIEMPO ES 18 MESES O ES 1.5 DEBIDO A QUE ESOS 18/12 ES DECIR 12 MESES QUE TIENE EL AÑO. ME SALE DOS RESPUESTA Y NO CUAL SEA SI EL 96% O EL 8%
¿A que tasa de interés mensual se debe poner un capital de 4900 dólares para que se convierta en un monto de 11956 en un tiempo de 3 semestres?
Francisco Gutiérrez Mora
el 20/12/16Francisco Gutiérrez Mora
el 20/12/16Ariel
el 20/12/16la verdad q ya me confundí, Yo vi los videos de Unicoos y es asi como usted los hizo, pero sucede que he pedido ayuda anteriormente en esta pagina y aplica de otra manera, y los resultados son muy diferente :( :( .
Por favor ayudeme con este tiene 2 respuestas diferente y no sé en realidad cual de las dos q me han dado los chicos de este grupo es la real
¿Calcular el monto que se genera si se establece un capital de 5100 dólares a una tasa de 8% de Interes Simple trimestral por un periodo de 13 bimestres?
Ariel
el 20/12/16Ángel
el 20/12/16A ver Ariel...
Calcular el monto que se genera si se establece un capital de 5100 dólares a una tasa de 8% de Interes Simple trimestral por un periodo de 13 bimestres
Interés simple=5100*0.08*(26/3)=5100*0.08*8,6666=3536 dólares
Monto=5100+3536=8636 dólares
((Si otra forma de calcular el monto te pareció más enrevesada no la uses, usa esta que te acabo de poner))
Ariel
el 20/12/16Ángel
el 20/12/16Ariel
el 20/12/16DEL EJERCICIO QUE ME AYUDO FRANCISCO NO ENTIENDO porque haces esto 7056=11956·R·18/1200 , esa es la formula del interes, perooo 11956 es el Monto, ahi deberia ser los 4900 q es el Capital, porque la formula es I=C*R*T/1200. AYUDAME CON ESO MATHS.
¿A que tasa de interés mensual se debe poner un capital de 4900 dólares para que se convierta en un monto de 11956 en un tiempo de 3 semestres?
Ángel
el 20/12/16En un rato te respondo, mírate esto mientras:
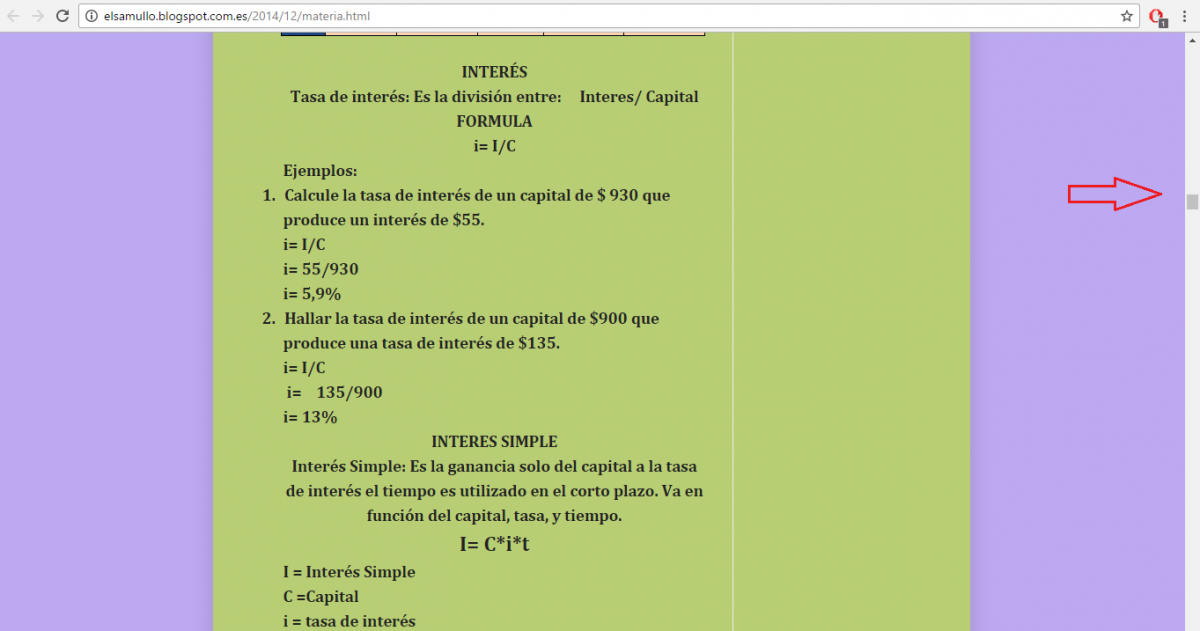
http://elsamullo.blogspot.com.es/2014/12/materia.html
Desde donde apunta la flecha hasta el final
Ángel
el 20/12/16¿A que tasa de interés mensual se debe poner un capital de 4900 dólares para que se convierta en un monto de 11956 en un tiempo de 3 semestres?
Monto=Capital+Interés11956=4900+Interés
Interés=7056 dólares
Interés=Capital*tasa de interés*tiempo <---------Fórmula general
Interés/(Capital*tiempo)=tasa de interés <---------------Mediante la fórmula general podemos averiguar la tasa de interés
7056/(11956*540/30)= 7056/(11956*18)= 7056/215208= 0.03279= 3.279 % mensual
7056/(11956*540/365)= 7056/(11956*1,48)= 7056/17688,33= 0.3989= 39,89 % anual
Ángel
el 20/12/16TODOS los ejercicios que has preguntado se resuelven con estas dos ecuaciones:
I=C*i*t
I=interés siemple
C=Capital
i=tasa de interés
t=tiempo
....De I=C*i*t puedes sacar estas:
C=I/i*t
i=I/c*t
t=I/c*i
Monto=Capital+Interés
...y puedes deducir estas:
Capital=Monto-Interés
Interés=Monto-Capital
Ariel
el 21/12/16Ángel
el 21/12/16¿A que tasa de interés mensual se debe poner un capital de 4900 dólares para que se convierta en un monto de 11956 en un tiempo de 3 semestres?
Datos que nos da el enunciado:
Monto=11956 dólares
Capital=4900 dólares
Monto=Capital+Interés
Interés=C*i*t
Datos nuevos que obtenemos con los datos del enunciado:
Monto=11956, Capital=4900, Monto=Capital+Interés --------------> 11956=4900+Interés -----------> Interés=7056
Interés=Capital*Tasa de interés*tiempo--------------------> Tasa de interés=Interés/(Capital*tiempo)
--------------------------> Tasa de interés= 7056/(11956*540/30) -------------------> Tasa de interés= 7056/(11956*18) -------------------> Tasa de interés= 7056/215208 --------------> Tasa de interés= 0.03279= 3.279 % mensual
COMO PUEDES OBSERVAR EL CAPITAL ES UN DATO QUE NOS DA EL ENUNCIADO, Y SU VALOR ES 4900
NADIE HA PODIDO DECIR CON RAZÓN QUE EL VALOR DEL CAPITAL SEA OTRO
Ariel
el 21/12/16Haz de pensar que soy bruto :( de verdad gracias pero este mañana veo como lo busco este valor 11956 me tiene tenso :( no entiendo, he tratado de analizarlo paso por pasoo pero sigo blokeado, te agradezco de todo corazón por tu tiempoo, y disculpa si te he hecho perder el tiempo
Ángel
el 21/12/16Ariel
el 21/12/16Brother eso yo si entiendo , lo que no entiendo es esto
Tasa de interés=Interés/(Capital*tiempo)
Tasa de interés= 7056/(11956*540/30)
Interes 7056 / Capital ??? (AKI ESTA EL PROBLEMA) porque 11956 y no 4900 ???? esa es mi confusión, EL TIEMPO SI LO ENTIENDO 18 MESES QUE CORRESPONDE A 3 SEMESTRE.
Ángel
el 21/12/16Ariel
el 21/12/16me he matadooooo todo el diaaa, porque a mi me salia 8% pero a ti te salia diferente, de igual gracias , pero si he aprendidoooo muchas gracias, espero y me ayudes con una pregunta que publique en el foto , es compuesto, puse la respuesta que me da a mi , espero y me digas si esta bn o errado para volver a intentarlo
-
hola podrían ayudarme con este ej de conteo? dice: un examen de matemática discreta consta de 20 proposiciones para responder verdadero o falso. El profesor acota que solo 8 de ellas son verdaderas. Con esta ayuda que da el profesor, ¿de cuantas maneras distintas puede un alumno completar el cuestionario? ¿y sin la ayuda?
-
Buenas tardes. No entiendo el paso que he encuadrado en azul. ¿Una ves completo cuadrados como continuo para llegar ahí? Muchas gracias por su atención.
-
NO ENTIENDO ES COMO DESCOMPONER LA TASA DE INTERES CON EL TIEMPO. AYUDEMEN POR FAVOR, ES INTERES SIMPLE
¿Calcular el monto que se genera si se establece un capital de 5100 dólares a una tasa de 8% de INTERES SIMPLE trimestral por un periodo de 13 bimestres?
Ángel
el 20/12/16Ariel
el 20/12/16Ariel
el 20/12/16lo q yo hacia es que la tasa de interes la aplicaba anual es decir si era 0.08 *4 porque era trimestral y asi la convertia anua, y uego aplicaba la formula que estan en los videos de unicoos. I=5100*0.32*26 /1200=35.36 YO DECIA Q ESE ERA EL INTERES Y LUEGO ESO LO SUMABA CON EL CAPITAL PARA OBTENER EL MONTO
Ariel
el 20/12/16Francisco Gutiérrez Mora
el 20/12/16Ariel
el 20/12/16mira eso es lo q no entiendo y me confundoo, puedo optar siempreee, por la tasa de interes colocarla anual, o depende del tiempo, porq utilizando esas formulas, yo tenia entendiido q la tasa de interes siempre tienen q estar anual, pero no se si solo es para el simple o tambn para el compuesto
Francisco Gutiérrez Mora
el 20/12/16Ariel
el 20/12/16Ariel
el 20/12/16Ariel
el 22/12/16 -
Me dan dos curvas c1 que esta definida en ec parametricas c1: x(theta) =1/2 + (1/2)cos(theta) y y(theta)= (1/2)sin(theta) y c2 que esta dada por r=3^(1/2)sin(theta)Me dan dos curvas c1 que esta definida en ec parametricas c1: x(theta) =1/2 + (1/2)cos(theta) y y(theta)= (1/2)sin(theta) y c2 que esta dada por r=3^(1/2)sin(theta) y me piden a)pasar c1 a polar y b) sacar el area de la region R, interior a ambas curvas.

De lo cual ya hice a donde me da una cardioide: 1/2 + 1/2 cos(theta) pero la interseccion solo se cumple en pi pero el otro punto de interseccion no puedo obtenerlo
quisiera saber si es que me salte un paso o hice algo erroneoAntonio Silvio Palmitano
el 20/12/16Te ayudo con las curvas.
Para la primera, designamos a su parámetro como t, a fin de no confundirnos con las coordenadas polares, con la que está expresada la ecuación de la segunda curva.
Observa que ambas curvas son circunferencias: la primera es tangente al eje coordenado OY en el origen, y la segunda es tangente al eje coordenado OX en el origen.
Observa que ambas curvas delimitan una región en el primer cuadrante, cuyos vértices son el origen y el punto de coordenadas:
A( 3/4 , 31/2/2 ).
Y observa, para cuando plantees el área de la región delimitada por ambas curvas, que deberás dividirla en dos regiones, separadas por la recta que pasa por el origen y por el punto A, y hacer el cálculo con coordenadas polares (recuerda que el área con coordenadas polares viene dada por la expresión: A = ∫ (1/2)r2dθ, con r expresado como función de θ).
Tienes las curvas cuyas ecuaciones son:
C1 (llamamos t a su parámetro):
x = 1/2 + (1/2)cost, haces pasaje de término y queda: x - 1/2 = (1/2)cost
y = (1/2)sent
elevas al cuadrado en ambas ecuaciones, sumas miembro a miembro y observa que son las ecuaciones cartesianas paramétricas, de una circunferencia
con centro c1(1/2,0) y radio r1 = 1/2, cuya ecuación cartesiana canónica es:
(x - 1/2)2 + y2 = 1/4,
luego desarrollas el binomio al cuadrado, haces pasaje de término, reduces términos semejantes y queda:
x2 + y2 - x = 0 (1).
C2(observa que tenemos su ecuación en coordenadas polares):
r = 31/2senθ, multiplicas por r en ambos miembros y queda:
r2 = 31/2rsenθ, sustituimos (recuerda las relaciones entre las coordenadas polares y las coordenadas cartesianas):
x2 + y2 = 31/2y (2),
haces pasaje de término, sumas 3/4 en amos miembros y queda:
(x - 31/2/2)2 + y2 = 3/4,
que es la ecuación de una circunferencia con centro c2( 31/2/2 , 0 ) y radio: r2 = 31/2/2.
Luego, con las ecuaciones señaladas (1) (2) tienes un sistema de dos ecuaciones con dos incógnitas que puedes resolver, y verás que sus soluciones son las coordenadas del origen y las coordenadas del punto A.
Queda para que hagas el cálculo del área pedida. Haz el intento, y si te es necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
Hola disculpen las molestias pero me podrian ayudar con el siguiente ejercicio es calculo :
Considere la curva C definida por x^(2/3)+y^(2/3)=a^(2/3) , a>0
a)Demuestre que la longitud de curva C definida, en el primer cuadrante esta dada por s=a^(1/3)de la integral definida de 0 hasta a de dx/x^(1/3)
b) Demuestre que la integral s converge y calcule su valor
en la parte a nose como trabjarla y en b me confunde por que para mi segun la p serie1/x^p deberia diverger con p>1 almenos que haya pasado algo por alto.
David
el 20/12/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
zas693
el 20/12/16Victoria vega
el 20/12/16Antonio Silvio Palmitano
el 20/12/16Tienes la expresión de una función cuadrática, cuya gráfica es una parábola, cuyo vértice tiene coordenadas: V( -b / 2a , c - b2 / 4a ).
Luego, la expresión de la derivada primera queda:
f ' (x) = 2ax + b, igualas a cero despejas y queda: x = - b / 2a, que es la abscisa de un punto crítico, posible máximo o posible mínimo.
Luego, la expresión del aderivada segunda queda:
f ' ' (x) = 2a, (observa que es constante) y observa tenemos dos casos:
a) si a es positivo, tenemos que la derivada segunda es positiva y, por lo tanto la función es cóncava hacia arriba en todo punto, y por lo tanto el punto crítico corresponde a un mínimo;
b) si a es negativo, tenemos que la derivada segunda es negativa y, por lo tanto la función es cóncava hacia abajo en todo punto, y por lo tanto el punto crítica corresponde a un máximo.
Espero haberte ayudado.