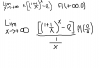-
David
el 5/12/16Echales un vistazo.. Funciones a trozos
Funcion a trozos Discontinuidad 01 Derivabilidad de una función a trozosA partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
HOLA CHICOS ALGUIEN PODRIA AYUDARME CON ESTE EJERCICIO: HALLAR LA LONGUITUD DE ARCO DE LA FUNCION Y=(4X-8)AL CUBO CON LIMITES ENTRE 0 Y 4
David
el 5/12/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Antonio Silvio Palmitano
el 5/12/16Has encontrado bien las raíces del desarrollo del determinante: D = -16 + m2, que son: m1 = 4, m2 = -4.
Luego, para valores de m distintos de 4 y de -4, tienes que el sistema de ecuaciones es compatible determinado y tiene solución única.
Luego, analizamos por separado:
Para m1 = 4, reemplazas y el sistema queda:
2x - 4y = 3
4x - 8y = 6,
divides por 2 en todos los términos de la segunda ecuación y el sistema queda:
2x - 4y = 3
2x - 4y = 3
observa que las dos ecuaciones son iguales, por lo que despejas: x = (3 + 4y)/2, y el sistema de ecuaciones es compatible indeterminado, y admite infinitas soluciones, que quedan expresadas: x = (3 + 4y)/2, y ∈ R.
Para m2 = -4, reemplazas y el sistema queda:
2x + 4y = 3
-4x- 8y = 6
dividimos por -2 en todos los términos de la segunda ecuación y el sistema queda:
2x + 4y = 3
2x + 4y = -3
observa que si restas miembro a miembro queda la identidad absurda: 0 = 6, y el sistema de ecuaciones es incompatible y no admite solución.
Espero haberte ayudado.
-
ORDEN DE DESPEJES PARA UNA FÓRMULA DE FÍSICA
DESPEJAR t DE
d=v0t+1/2at2
Antonio Silvio Palmitano
el 5/12/16Tienes la expresión (escribimos de derecha a izquierda a partir de tu enunciado:
(1/2)at2 + v0t = d, multiplicamos en todos los términos de la ecuación por 2/a y queda:
t2 + (2/a)v0t = 2d/a, ordenamos factores en el segundo término del primer miembro y queda:
t2 + 2*t*(v0/a) = 2d/a, sumamos en ambos miembros: (v0/a)2 y queda:
t2 + 2*t*(v0/a) + (v0/a)2 = 2d/a + (v0/a)2,
factorizamos el primer miembro (observa que tenemos un trinomio cuadrado perfecto), resolvemos el segundo término del segundo miembro y queda:
(t + v0/a)2 = 2d/a + v02/a2, extraemos denominador común en el segundo miembro y queda:
(t + v0/a)2 = (2ad + v02)/a2, hacemos pasaje de potencia como raíz, distribuimos la raíz en el segundo miembro y queda:
t + v0/a = ± √(2ad + v02) / a, hacemos pasaje de término y queda:
t = - v0 / a ± √(2ad + v02) / a, extraemos denominador común y llegamos a:
t = ( - v0 ± √(2ad + v02 ) / a.
Espero haberte ayudado.
-
David
el 5/12/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Buenas tardes. Tengo una duda con una actividad en la que no entiendo su resolucion. Hay que estudiar la convergencia o divergencia de la serie de la imagen. En su resolucion me indican estos pasos que pongo debajo pero no entiendo como se llega a 1-1/(n+1). Muchas gracias por su ayuda.
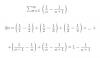
Antonio Silvio Palmitano
el 5/12/16Debes plantear la sucesión de sumas parciales. Planteamos algunos de sus elementos:
S1 = a1 = 1 - 1/2
S2 = S1 + a2 = 1 - 1/2 + 1/2 - 1/3 = 1 - 1/3
S3 = S2 + a3 = 1 - 1/3 + 1/3 - 1/4 = 1 - 1/4
S4 = S3 + a4 = 1 - 1/4 + 1/4 - 1/5 = 1 - 1/5
y en general, observando los números de orden y los denominadores en los términos fraccionarios, queda para el elemento general de la sucesión de sumas parciales:
Sn = 1 - 1/(n + 1).
Luego, estudiamos la convergencia o divergencia de la serie mediante el límite del elemento general de la sucesión de sumas parciales:
Lím(n->inf) Sn = Lím(n->inf) ( 1 - 1/(n + 1) ) = 1 - 0 = 1, por lo que concluimos que la serie converge a uno.
Espero haberte ayudado.
-
¿como puedo mandar imagenes? siempre que envio se hacen muy pequeñas, utilizo picasion ya que me piden URL
-
Hola Buenas quisiera que me ayudaran con este limite... hice el estudio de (1 + 1/x) elevado a la x y me da e.... pero quede en el paso que deje de segundo... es por lhopital muchas gracias
-
Buenas, me podrían por favor ayudar con este ejercicio que mañana tengo final y no me sale? Muchas Gracias!!
Antonio Silvio Palmitano
el 5/12/16Planteamos la combinación lineal nula para los vectores del conjunto A:
a<1,1,0,4> + b<1,2,3,0> + c<3,4,3,k2-1> = <0,0,0,0>
luego resolvemos componente a componente y queda el sistema de ecuaciones:
a + b + 3c = 0
a + 2b + 4c = 0
3b + 3c = 0, de aquí podemos despejar: c = -a (1)
4a + (k2-1)c = 0
sustituimos en las demás ecuaciones, reducimos términos semejantes y queda:
-2a + b = 0, de aquí podemos despejar: b = 2a (2)
-3a + 2b = 0
(4 - (k2-1))a = 0
sustituimos en la demás ecuaciones (en realidad solo en la segunda), reducimos términos semejantes y queda:
a = 0
(4 - (k2-1))a = 0
observa que al reemplazar en la última ecuación queda la identidad verdadera 0 = 0 para cualquier valor real k, y luego, al sustituir en las ecuaciones señaladas (2) y (1) tenemos:
b = 0
c = 0,
por lo que concluimos que los tres vectores del conjunto A son linealmente independientes para todo número real k.
Observa que A no puede ser base de R4, porque el espacio vectorial R4 tiene dimensión 4, y una base suya debe tener cuatro vectores linealmente independientes.
Por lo tanto, podemos asegurar que el conjunto A es base de un subespacio vectorial de R4, cuya dimensión es tres.
Espero haberte ayudado.
-
El problema es: Supongamos que eres un ingeniero de seguridad de una compañía química industrial y estás diseñando un área de decantación para los desechos químicos. Se localiza en un bote rectángular que tiene 200 yardas de largo y 75 yardas de ancho. El área de decantación debe tener 10,000 yardas cuadradas. Habrá una zona de seguridad de ancho uniforme alrededor del perímetro de área de decantacióon. a) sea a el ancho de la zona de seguridad. Escribe expresiones para el largo y el ancho del área de decantación interior, en término de a y del largo y ancho total. b)Escribe una ecuación para el área de la región de decantación, usando el área específica de 10,000 yardas cuadradas y el producto del largo y ancho de la parte a. c) Multiplica y simplifica los términos de la ecuación para llegar a una ecuación cuadrática en la forma ax2+bx+c=0. d) Identifica a, b y c. Después usa la fórmula cuadrática para determinar el ancho (a) de la zona de seguridad que verifica la ecuación.
Gracias por la ayuda de antemano. :) Me han ayudado bastante. :)David
el 6/12/16Lo siento pero me pierde el enunciado. no sé lo que es el area de decantación.. Por otro lado, es imposible ayudarte si no envías por lo menos un dibujo...
Se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)