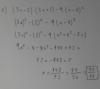Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Marta
el 4/12/16

Buenas no me sale el apartado b y c podrías ayudarme?
Gracias

••0 voto/s
•
Ángel
el 4/12/16

•1 voto/s
•
Marta
el 4/12/16
Muchas gracias, muy útil :)

•0 voto/s
•
Ángel
el 4/12/16
De nada :D
Te va el c)

•1 voto/s
•
Ángel
el 4/12/16
Observa que la solución simplificada al máximo sería: 18x-37, que es lo que te piden en el ejercicio
Para hallar el valor de x simplemente harías como te indiqué en el documento adjunto x=37/18 (al igualar a cero)

•1 voto/s
•

Cancelar
Marcos
el 4/12/16

Hola, como ruesuelvo este ejercicio? Desde ya muchas gracias
Dados los puntos (-1,2,4) ,(1,-2,1) y (1,1,1) obtener la ecuación paramétrica e implícita del plano que contenga esos tres puntos.

••0 voto/s
•
Lucía
el 4/12/16
No se si está mal escrito, pero un punto en el eje xy sólo puede tener dos números: (x,y)

•0 voto/s
•
Adrián
el 4/12/16
Vamos allá, Marcos.
Para determinar un plano, ¿qué necesitas? Un punto y dos vectores direccionales de dicho plano (es decir, dos vectores que sean linealmente independientes entre sí). Si tienes tres puntos, el ejercicio es muy fácil. Vamos a llamar a los puntos que te dan A=(-1,2,4), B=(1, -2,1) y C=(1,1,1)
Calculamos un vector direccional, por ejemplo el AB=(1,-2,1) - (-1,2,4) = (2,-4,-3)
Calculamos otro vector direccional, por ejemplo CB=(1,-2,1) - (1,1,1) = (0,-3,0)
Ya tienes dos vectores que son linealmente independientes (no dependen el uno del otro), ¿qué nos falta? Un punto. Y un punto puede ser cualquiera de los tres que tienes: A, B, o C.
Aplicas las ecuaciones paramétricas de un plano sustituyendo los datos que tienes y luego puedes obtener la ecuación implícita.

•1 voto/s
•
Marcos
el 4/12/16
Perfecto, gracias Adrian.

•0 voto/s
•
David
el 5/12/16
Ecuación del plano
•0 voto/s
•

Cancelar
juan
el 4/12/16

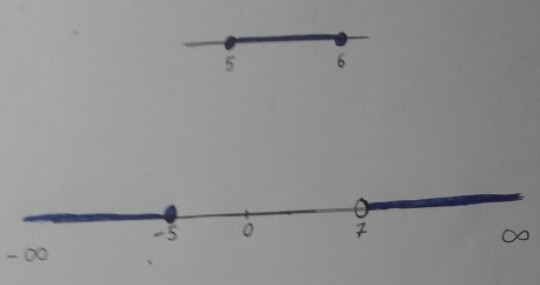
Alguien que me ayude escribir en forma de intervalo

Comprendidos entre 5 y 6 ambos incluidos
Mayores que 7 menores o iguales que -5

Gracias de ante mano

••0 voto/s
•
Ángel
el 4/12/16
Comprendidos entre 5 y 6 ambos incluidos -----> [5,6]
Mayores que 7 menores o iguales que -5 ---------> (-infinito, -5] U (7, infinito)

•0 voto/s
•

Cancelar
Alejandro Expósito
el 4/12/16

Sean A=7/3−5/7×7/9 y B=(1/4−1)² Demuestra que A•B=1
¿Alguien me ayuda a resolverlo?

••0 voto/s
•
Ángel
el 4/12/16
Escríbelo correctamente para ayudarte

•0 voto/s
•

Cancelar
lbp_14
el 4/12/16

Hola Unicoos,
El enunciado dice que hay que demostrar que la ecuación trigonométrica de como resultado 1+sen2x
Me podrían ayudar paso a paso, me he quedado atascada.
Muchas gracias.

••0 voto/s
•
Ángel
el 4/12/16

•1 voto/s
•

Cancelar
Isabel
el 4/12/16

Hola, ¿alguien podría ayudarme con este ejercicio?, os envío lo que tengo , pero me tiene atascada, gracias.

••0 voto/s
•
David
el 5/12/16
¿cual es tu duda?....

•0 voto/s
•
Isabel
el 6/12/16
A ver la respuesta que tengo dudas es la n.5 de la tarea, las otras ya las he resuelto, pero en esa no tengo claro como localizar las coordenadas paralelas geográficamente, con las dadas en los pueblos del ejercicio.

•0 voto/s
•

Cancelar
lbp_14
el 4/12/16

Hola Unicoos,
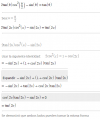
Me podrían echar una mano con esta ecuación trigonométrica paso a paso, el enunciado dice que hay que demostrar que su resultado sea tgx
Muchas gracias.

••0 voto/s
•
Antonio Silvio Palmitano
el 4/12/16
Por favor, verifica que la expresión inicial esté correctamente escrita para que podamos ayudarte.

•1 voto/s
•
lbp_14
el 4/12/16
El enunciado es lo que está escrito en color rojo y hay que demostrar que dé como resultado tgx

•0 voto/s
•
Ángel
el 4/12/16

Si dudas en algún paso dimelo, porque la solución desarrollada es muy larga

•1 voto/s
•

Cancelar
Alejandro Expósito
el 4/12/16

Una colección de discos 1/3 son de Beethoven y 2/5 de Mozart y 42 de Bach ¿Cuántos hay en total?
¿Me ayuda alguien?

••0 voto/s
•
Antonio Silvio Palmitano
el 4/12/16
Por favor, verifica que el enunciado esté correctamente escrito para que podamos ayudarte.

•0 voto/s
•
Ángel
el 4/12/16
1/3*x + 2/5*x+42= x
Pasamos a común denominador (mcm: 15)
5x/15+6x/15+630/15=15x/15
Quitamos denominadores:
5x+6x+630=15x
Agrupamos "x"
630=4x
Resolvemos:
x=157,5 discos en total
(((es raro que en este tipo de ejercicios te dé resultado decimal)))

•0 voto/s
•
Lucía
el 4/12/16
Si queda decimal como está expresado arriba, deberías poner el número sin los decimales, es decir, 157.

•0 voto/s
•

Cancelar
Ana
el 4/12/16

hay una operacion que no logro solucionar y me gustaria que me expliqueis como se podria resolver:
2√48 - 3√675 +√588

••0 voto/s
•
Antonio Silvio Palmitano
el 4/12/16
Comienza por factorizar como producto de números naturales primos a todos los argumentos de las raíces:
√(48) = √(2⁴*3) = distribuyes = √(2⁴)*√(3) = simplificas = 2²*√(3) = 4*√(3);
√(675) = √(3²*3*5²) = distribuyes y ordenas = √(3²)*√(5²)*√(3) = simplficas = 3*5*√(3) = 15*√(3);
√(588) = √(2²*7²*3) = distribuyes = √(2²)*√/7²)*√(3) = simplifias = 2*7*√(3) = 14*√(3);
luego pasas e la expresión del enunciado:
2√(48) - 3√(675) + √(588) = reemplazas:
= 2*4*√(3) - 3*15*√(3) + 14*√ (3) = resolvemos factores racionales:
= 8*√(3) - 45*√(3) + 14*√(3) = resolvemos:
= - 23*√(3).
Espero haberte ayudado.

•1 voto/s
•
Ana
el 4/12/16
gracias por tener un rato para explicarmelo, ha sido muy amable

•0 voto/s
•

Cancelar
miguel
el 4/12/16

Como hacer una ecuación matricial de 2.x-c. D=(I+D). C la identidad es de orden 3 también hay otra ecuación matricial q no di en clase Ax+BA=B espero k lo hayan entendido gracias :)

••0 voto/s
•
Ángel
el 4/12/16
Manda el enunciado original

•1 voto/s
•

Cancelar