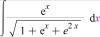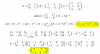-
juan
el 3/12/16No logró hacerlo....
Encontrar el volumen sólido obtenido al girar limitada por las curvas alrededor del eje y . Grave un esquema de la región del sólido y de un disco tipico
Y=4x-x^2
X=4
X=0
MI problema es que no pude despejar x para que lo hay girar en y .....
Antonio Silvio Palmitano
el 4/12/16Vamos con la ayuda para tratar con la primera ecuación, cuya gráfica es una parábola con eje x = 4 y vértice V(2,4), raíces 0 y 4, luego tienes:
y = 4x - x2, haces pasajes de términos y queda:
x2 - 4x = - y, luego sumas 4 en ambos miembros y queda:
x2 - 4x + 4= 4 - y, luego factorizas el primer miembro (observa que tienes un trinomio cuadrado perfecto):
(x - 2)2 = 4 - y, luego haces pasaje de potencia como raíz y queda:
x - 2 = ±√(4 - y), luego haces pasaje de término y queda:
x = 2 ±√(4 - y), luego observa que tienes una ecuación para cada rama de la parábola:
a) para la rama derecha ( con x entre 2 y 4): x = 2 + √(4 - y),
b) para la rama izquierda ( con x entre 0 y 2): x = 2 - √(4 - y),
Luego, observa que el intervalo de integración es: 0 ≤ y ≤ 4. y que para calcular el volumen del sólido de revolución alrededor del eje OY (V) debes plantear una diferencia entre volúmenes: volumen generado por la rama derecha (Vd) menos volumen generado por la rama izquierda (Vi). Luego tenemos:
Vd = π ∫ ( 2 + √(4 - y) )dy, para evaluar entre 0 y 4;
Vi = π ∫ ( 2 - √(4 - y) )dy, para evaluar entre 0 y 4;
y una vez hechos los cálculos, queda:
V = Vd - Vi .
Espero haberte ayudado.
-
Alba
el 3/12/16 -
Miguel Guerra
el 3/12/16Una duda rápida, en un ejercicio de álgebra lineal, me pide calcular las bases del núcleo y la imagen de una aplicación lineal, la base del núcleo me sale el vector nulo (0, 0), ¿es posible que me salga esa base para Ker(f) o estoy haciendo algo mal?
Gracias de antemano.
-
Lenin Molina
el 3/12/16
Hola, buenas tardes, quisiera que me ayudaran con esta integral en la que no se como completar cuadrados con el numero e
Wolfram Alpha la hace mal. Gracias de Antemano
Antonio Silvio Palmitano
el 3/12/16Debes comenzar con la sustitución (cambio de variable): w = ex, de donde tienes: dw = exdx, luego sustituyes y queda:
I = ∫ ( 1/√(1+w+w2) )dw (1).
Luego, pasamos al argumento de la raíz:
1 + w + w2 = sumamos y restamos 1/4, agrupamos términos y queda:
= (1/4 + w + w2) - 1/4 = factorizamos el agrupamiento:
= (1/2 + w)2 - 1/4.
Luego planteamos la sustitución: z = 1/2 + w, de donde tenemos: dz = dw, sustituimos en la expresión señalada (1) y queda:
I = ∫ ( 1/√(z2 - 1/4) )dz (2).
Luego, puedes continuar con la sustitución trigonométrica: z = (1/2)sec2t,
Haz el intento de continuar, y si te es necesario, puedes volver a consultar.
Espero haberte ayudado.
-
lautaro
el 3/12/16No puedo resolver el siguiente problema de algebra lineal (unidad : cambio de bases), si alguno lo puede resolver o me puede orientar se los agradecería mucho.
Sea (O´,X´´Y´´) el sistemas de coordenadas que se obtiene rotando el sistema (O,XY), asociado a la base canónica, en un angulo de 60º y trasladando el origen al punto O´(1, -2). Sea P(3, -4) y la recta L1: x + 2y +1=0, en el sistema (O,XY) y la recta de forma parametrica L2 : { x´´: 1 + √3µ µ εR , en el sistema (O´,X´´Y´´)
{ y´´: µ
A) Hallar en el sistema (O,XY) la ecuacion implicita de la recta L3 que es paralela a L2 y pasa por P.
B) Calcular, en el sistema (O´,X´´Y´´), las coordenadas del punto en que intersectan L1 y L3 .
David
el 5/12/16Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Jacin
el 3/12/16¿Cómo resolver la siguiente ecuación matricial ?
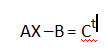
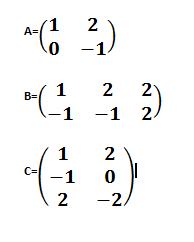
Antonio Silvio Palmitano
el 3/12/16Tienes la ecuación matricial:
AX - B = Ct, haces pasaje de término y queda:
AX = Ct + B.
Luego, debes calcular la matriz inversa de la matriz A (observa que A es invertible porque su determinante es igual a -1 que es distinto de cero), y multiplicar en ambos miembros por izquierda por ella (A-1), y queda:
A-1AX = A-1(Ct + B), luego resuelves el producto entre los dos primeros factores del primer miembro (su resultado es la matriz identidad de orden 2) y queda:
I2X = A-1(Ct + B), luego resolvemos el primer miembro (recuerda que la matriz identidad es neutra para le producto) y queda:
X = A-1(Ct + B).
Luego, queda que hagas todos los cálculos.
Espero haberte ayudado.
-
Carlos Ojeda
el 3/12/16 -
lbp_14
el 3/12/16 -
Marcos
el 3/12/16Hola tengo una duda de universidad. El ejercicio me pide:
Determinar el orden del polinomio de Taylor de f(x)= √(36+x)centrado en 0 que permita aproximar √35 con un error menor que 10-4.
No me dejan usar la calculadora. Pero el problema es que no se cual va a ser el resultado a devolver. Si me pudieran ayudar se los agradecería muchisimo.
David
el 5/12/16Echale un vistazo a este vídeo que grabé como excepcion... Polinomio de Taylor con Resto de una funcion trigonometrica
O a este, que se parece... Polinomio de McLaurin de una función exponencialA partir de ahí, me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Daniel Diego
el 3/12/16Hola buenos días necesito ayuda en el siguiente problema trigonométrico, me quedé atascado casi al final del ejercicio y no consigo resolverlo, dice lo siguiente:
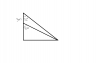
Una escultura de 3m de altura esta situada sobre un prisma de piedra. Desde el punto de la horizontal que pasa por la base del prisma se miden los ángulos de observación al extremo superior del prisma y de la estatua, que son 32º y 47º, respectivamente. Encuentra la altura del prisma y la distancia horizontal desde el punto de observación al prisma.
Planteado seria así:
Lucía
el 3/12/16
Antonio Silvio Palmitano
el 3/12/16Observa que tienes dos triángulos rectángulos, cuyas bases coinciden, por lo que llamamos x a la base compartida.
Luego, llamamos y a la longitud de la altura del triángulo rectángulo más pequeño, y observa que la altura del triángulo rectángulo más grande es: (y + 3).
Luego planteamos:
tan(47°) = (y+3)/x (en el triángulo rectángulo más grande), de donde puedes despejar: x = (y+3)/tan(47°) (1),
tan(32°) = y/x (en el triángulo rectángulo más pequeño), de donde puedes despejar: x = y/tan(32°) (2),
luego igualas y tienes la ecuación:
(y+3)/tan(47°) = y/tan(32°), haces pasajes de divisores como factores y queda:
(y+3)tan(32°) = ytan(47°), distribuyes en el primer miembro de la ecuación y queda:
y tan(32°) + 3tan(32°) = ytan(47°), haces pasajes de términos y queda:
ytan(32°) - ytan(47°) = - 3tan(32°), extraes factor común en el primer miembro y queda:
y( tan(32°) - tan(47°) ) = - 3tan(32°), haces pasaje de factor como divisor y queda:
y = - 3tan(32°)/( tan(32°) - tan(47°) ).
Luego, solo queda que hagas el cálculo y luego reemplaces en las ecuaciones señaladas (1) (2) para obtener el valor de x.
Espero haberte ayudado.
