-
Buenas tardes.
Espero que alguien me pueda ayudar con este planteamiento, muchas gracias.
Será
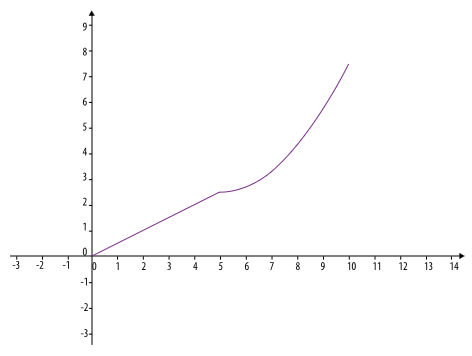
necesario que analices la siguiente gráfica que representa una
función de la posición de un objeto con respecto del tiempo: en el eje x
se encuentra el tiempo en minutos, en el eje y se encuentra su posición
en el momento t (tiempo).¿Qué velocidad lleva el objeto los primeros cinco minutos?
Antonio Silvio Palmitano
el 2/12/16Observa que para el intervalo de t que va de t = 0 a t =5, la gráfica de la función es un segmento (pedazo de recta), que une los puntos de coordenadas (0;0) y (5;2,5), este último con su ordenada aproximada. Luego, la pendiente de la recta que incluye al segmento es:
m = (x2 - x1)/(t2 - t1) = (2,5 - 0)/(5 - 0) = 2,5/5 = 0,5. Luego, tomamos como punto de referencia al origen, y tenemos la ecuacion cartesiana de la recta:
x = m(t - t1) + x1, que al reemplazar valores queda: x = 0,5t, con 0 < t < 5.
Luego, como la gráfica tiempo-posición es un tramo recto para este intervalo, tenemos que la velocidad es constante, e igual a 0,5, que es la pendiente de la recta que incluye al segmento, por lo tanto concluimos:
v = 0,5, con las unidades que correspondan.
Espero haberte ayudado.
. -
sec(β): -2 π∠B∠3π/2
Dice que B pertenece al tercer cuadrante? ¿Cómo sé yo eso si en el tercer cuadrante el coseno también es negativo y la secante por tanto también lo sería?
Muchas gracias
Antonio Silvio Palmitano
el 1/12/16Tal como dices, en el tercer cuadrante solo la tangente y la cotangente toman valores positivos, y las demás toman valores negativos.
Si tienes los datos de tu enunciado, efectivamente el ángulo β pertenece al tercer cuadrante, y para encontrar los demás valores puedes emplear las identidades:
cosΒ = 1/secβ = 1/(-2) = -1/2;
senβ = - √(1 - cos2β) = - √(1 - (-1/2)2) = - √(1 - 1/4) = - √(3/4) = - √(3)/√(4) = - √(3)/2;
tanβ = senβ/cosβ = (- √(3)/2) / (-1/2) = √(3);
cotgβ = 1/tanβ = 1/√(3) = ( 1*√(3) )/( √(3) )2 = √(3)/3;
cosecβ = 1/senβ = 1/(- √(3)/2) = - 2/√(3) = - ( 2*√(3) )/ ( √(3) )2 = - 2√(3)/3.
Espero haberte ayudado.
carmela
el 2/12/16Antonio Silvio Palmitano
el 2/12/16 -
Antonio Silvio Palmitano
el 2/12/16Vamos con algunas ayudas (los gráficos los dejo para que los hagas).
IIb) Observa que piden estudiar continuidad en el punto de corte, por lo que debemos emplear la definición:
1°) f(1) = evaluamos en el segundo trozo = 2(1) - 6 = - 4 (la función está definida en el punto).
2°) Límites laterales:
Lím(x->1-) f(x) = Lïm(x->1-) (x2 - 5x) = 1 - 5 = -4;
Lím(x->1+) f(x) = Lïm(x->1+) (2x - 6) = 1 - 5 = -4;
luego, como ambos coinciden, tenemos:
Lím(x->1) f(x) = - 4 (la función tiene límite en el punto).
3°) Como el valor de la función en el punto coincide con el límite en el punto, concluimos que la función es continua en el punto de corte x = 1.
III) Tienes el polinomio: P(x) = -2x2 + nx + q, y los siguientes datos:
"el resto al dividir por (x - 2) es 20, por lo que aplicamos el Teorema del Resto y queda:
P(2) = 20, evaluamos el polinomio y queda:
- 8 + 2n + q = 20, hacemos pasaje de término y queda la ecuación:
2n + q = 28 (1);
"4 es raíz del polinomio", por lo que aplicamos el Teorema del Resto y queda:
P(4) = 0, evaluamos el polinomio y queda:
-32 + 4n + q = 0, hacemos pasaje de término y queda la ecuación:
4n + q = 32 (2);
luego planteamos el sistema formado por las ecuaciones señaladas (1) (2):
2n + q = 28
4n + q = 32
resuelves el sistema, y su solución es: n = 2, q = 24;
luego el polinomio queda expresado: P(x) = -2x2 + 2x + 24.
IIIb) Para factorizarlo, observa que su coeficiente principal es a = -2, y planteas la ecuación:
P(x) = 0, reemplazas y queda:
-2x2 + 2x + 24 = 0, divides en todos los términos por -2 y queda:
x2 - x - 12 = 0, observa que es una ecuación polinómica cuadrática, aplicas la fórmula resolvente y tienes las raíces: x1 = 4 (que es dato del enunciado) y x2 = -3.
Luego pasamos a la factorización para un polinomio cuadrático: P(x) = a(x - x1)(x - x2), reemplazamos valores y queda:
P(x) = -2(x - 4)(x + 3).
IVA) Tenemos la inecuación: (2x - 6)2(8 - x) < 0, y observa que el primer factor en el primer miembro siempre es positivo (es un cuadrado), por lo que tenemos como única opción que el segundo factor sea negativo, para que el producto nos de negativo como exige la inecuación, por lo tanto planteamos:
8 - x < 0, hacemos pasaje de término y queda:
- x < - 8, multiplicamos por -1 en ambos miembros (observa que cambia el sentido de la desigualdad) y queda:
x > 8, por lo que el conjunto solución expresado como intervalo queda: S = (8,+inf).
IVB) Tenemos la ecuación:
3(2x - 5) = 9, distribuimos en el primer miembro y queda:
6x - 15 = 9, hacemos pasaje de término, resolvemos el segundo miembro y queda:
6x = 24, hacemos pasaje de factor como divisor, resolvemos el segundo miembro y queda:
x = 4.
Va) Interpretamos que el gráfico continúa indefinidamete hacia la izquierda y hacia la derecha.
Dominio: D = (-inf,+inf) = R;
raíces (cortes con el eje OX): x1 = - 5, x2 = 2 y x3 = 4,5 (esta última aproximada);
signo (intervalos entre raíces:
la función es positiva (la gráfica está por encima del eje OX) en: (-inf , -5) u (2 , 4,5),
la función es negativa (la gráfica está por debajo del eje OX) en: (-5 , 2) u (4,5 , +inf);
ordenada al origen (ordenada del punto de corte con el eje OY): b = -3.
Vb) Vamos con los intervalos:
f es creciente en: (-3 , 3,5) (el valor del extremo derecho lo hemos aproximado),
f es decreciente en: (-inf , -3) u (3,5 , +inf),
f presenta Mínimo en x = -3 (pasa de decrecer a crecer en este punto), y es Local, porque no es el punto "más bajo" de todo el gráfico,
f presenta Máximo en x = 3,5 (pasa de crecer a decrecer en este punto), y es Local, porque no es el punto "más alto" de todo el gráfico.
c) Vamos con los límites:
Lím(x->-inf) f(x) = +inf (a medida que nos ubicamos "más a la izquierda" en el gráfico, la curva se ubica "cadavez más arriba" en el gráfico,
Lím(x->+inf) f(x) = -inf (a medida que nos ubicamos "más a la derecha" en el gráfico, la curva se ubica "cada vez más abajo" en el gráfico.
Espero haberte ayudado.
-
 Buenas noches. En este ejercicio alfa es del segundo cuadrante. Cómo hallo lo que me piden si 180+alfa está referido al primer cuadrante?
Buenas noches. En este ejercicio alfa es del segundo cuadrante. Cómo hallo lo que me piden si 180+alfa está referido al primer cuadrante?Antonio Silvio Palmitano
el 1/12/16Puedes plantear el coseno del ángulo, que es negativo en el segundo cuadrante:
cosα = - √(1 - sen2α) = - √(1 - 16/25) = - √(9/25) = - 3/5.
Luego, puedes plantear la expresión del seno de la suma de dos ángulos:
sen(180° + α) = sen(180°)*cosα + cos(180°)*senα = resolvemos y reemplazamos valores:
= 0*(-3/5) + (-1)*(4/5) = resolvemos en cada término:
= 0 - 4/5 = - 4/5.
Espero haberte ayudado.
M gales
el 1/12/16Yo calcularía el ángulo con el arco cuyo seno en 4÷5 y eso me da 53 grados 7minutos y 48,37 segundos y con ese ángulo sustituyo 180 grados más ese ángulo y eso me dará el ángulo en él tercer cuadrante, que sería negativo. Y no dice que esta en el segundo cuadrante necesariamente, solo que el ángulo no esta en el primero.
Espero que te sirva y haberme explicado bien!!
Antonio Silvio Palmitano
el 2/12/16Dices en tu enunciado (transcribimos): "En este ejercicio alfa es del segundo cuadrante", por lo tanto se cumple la desigualdad doble:
90° < α < 180°,
luego, para ubicar en cuál de los cuadrantes se ubica el ángulo (180° + α), sumamos 180° en los tres miembros de la desigualdad doble y queda:
180° + 90° < 180° + α < 180° + 180°, resolvemos en el primero y el tercer miembro y llegamos a:
270° < (180° + α) < 360°,
que nos indica que el ángulo (180° + α) pertenece al cuarto cuadrante.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 1/12/16Planteamos los límites laterales:
Lím(x->0-) f(x) = Lím(x->0-) ( asen(2x)/x + (x + 1)b ) = separamos en términos:
= Lím(x->0-) asen(2x)/x + Lím(x->0-) (x + 1)b = extraemos factores constantes:
= a Lím(x->0-) sen(2x)/x + b Lím(x->0-) (x + 1) = multiplicamos y dividimos por 2 en el primer límite:
= 2a Lím(x->0-) sen(2x)/(2x) + bLím(x->0-) (x + 1) = resolvemos (el primer límite lo has visto en clase):
= 2a*1 + b*1 = 2a + b.
Lím(x->0+) f(x) = Lím(x->0+) (a(x2 + 1) + 3b) = resolvemos: = a + 3b.
Luego, para que exista el límite para x tendiendo a cero, igualamos los resultados de los límites laterales y queda:
2a + b = a + 3b, hacemos pasajes de términos, reducimos términos semejantes y queda:
a = 2b, por lo que concluimos que a debe ser el doble de b, y b puede ser cualquier número real.
Luego resumimos, según la definición de continuidad (reemplazamos a por 2b):
1°) f(0) = evaluamos en el segundo trozo: = 2b(02 + 1) + 3b = 5b.
2°) Lím(x->0) f(x) = 5b (observa que éste es el resultado de los dos límites laterales).
3°) f es continua en x = 0, si a = 2b, con b ∈ R.
Espero haberte ayudado.