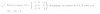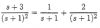-
hola soy juan cancho me gustaria que alguien me pusiera ejercicios de intervalos semirecta de iracionalizacion de raices y radicales gracias.
David
el 5/12/16Si nos dejas algun ejemplo de lo que te preocupa, podremos recomendarte ejercicios.
P.D. Si eres unicoo PRO (http:/www.unicoos.com/planes) encontrarás ejercicios resueltos paso a paso para practicar en el "material adicional" que acompaña a todos los vídeos. Un abrazo!... -
Hola! Necesito ayuda con este ejercicio, en los posible en su totalidad, muchas gracias!
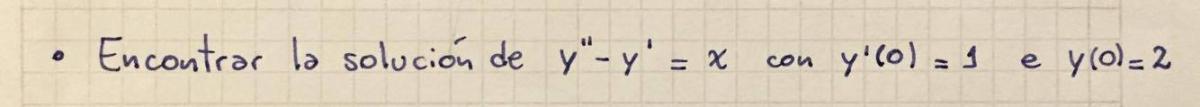
Antonio Silvio Palmitano
el 4/12/16Tienes una ecuación diferencial de segundo orden, de primer grado y lineal, que no es homogénea. Planteamos para su solución general la suma de la solución de la ecuación homogénea más una solución particular: y = yh + yp (1).
1°) Planteamos la ecuación homogénea:
y ' ' - y ' = 0, su ecuación característica queda:
r2 - r = 0,cuyas soluciones son: r1 = 0, que corresponde a la familia de funciones polinómicas, r2 = 1, que corresponde a una familia de funciones exponenciales; luego planteamos su solución:
yh = ae0x + be1x, resolvemos exponentes y queda:
yh = a + bex (2), con a y b constantes.
2°) Planteamos la solución particular:
yp = x(Ax + B) = Ax2 + Bx (2), con A y B constantes a determinar, y observa que es una expresión polinómica con un grado más que la expresión no homogénea, debido a que tenemos a la familia de los polinomios representada en la solución general;
luego derivamos dos veces y quedan:
yp' = 2Ax + B,
yp' ' = 2A,
luego sustituimos en la ecuación diferencial del enunciado y queda:
2A - ( 2Ax + B) = x, distribuimos, ordenamos términos y queda:
- 2Ax + (2A - B) = 1x + 0, luego comparamos términos semejantes y queda el sistema de ecuaciones:
- 2A = 1
2A - B = 0,
cuya solución es: A = - 1/2, B = - 1,
luego reemplazamos en la ecuación señalada (2) y queda la expresión de la solución particular:
yp = - (1/2)x2 - 1x = - (1/2)x2 - x (3).
3°) Sustituimos las expresiones señaladas (2) (3) en la ecuación señalada (1) y tenemos la expresión de la solución general de la ecuación diferencial:
y = a + bex - (1/2)x2 - x, con a ∈ R y b ∈ R (4).
4°) Luego tenemos las condiciones iniciales: y(0) = 2, y ' (0) = 1, y para tratar con ellas derivamos en la expresión señalada (4) y queda:
y ' = bex - x - 1 (5), luego evaluamos las expresiones señaladas (4) (5) con las condiciones iniciales (x = 0, y = 2, y ' = 1) y queda el sistema de ecuaciones:
a + b =2
b - 1 = 1,
cuya solución es: a = 0, b = 2,
por lo que la solución de la ecuación diferencial con las condiciones iniciales indicadas en el enunciado queda (reemplazamos en la ecuación señalada (4)):
y = 2ex - (1/2)x2 - x.
Luego, puedes verificar que la solución es válida planteando las derivadas primera y segunda y sustituyendo en la ecuación diferencial del enunciado.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 4/12/16Planteamos la matriz: M - kI:
(1-k) 0 -2
0 -k 0
-2 0 (4-k),
luego desarrollamos su determinante (por ejemplo con la Regla de Sarrus) y queda:
|M - kI| = (1-k)(-k)(4-k) - (-2)(-k)(-2) =
= - k(1 - k)(4 - k) + 4k =
= - k(4 - 5k + k2) + 4k =
= - 4k + 5k2 - k3 + 4k =
= - k3 + 5k2.
Luego planteamos la ecuación del enunciado:
- k3 + 5k2 = 0, extraemos factor común en el primer miembro y queda:
k2(- k + 5) = 0, luego, por anulación de un producto, tenemos dos opciones:
a) k2 = 0, cuya solución es: k = 0 (observa que es una raíz cuya multiplicidad es 2),
b) - k + 5 = 0, cuya solución es: k = 5.
Espero haberte ayudado.
-
hola, me pueden decir porque esta afirmacion es falsa? existe un sistema de 6 ecuaciones con 5 incognitas que es incompatible
Antonio Silvio Palmitano
el 4/12/16La afirmación es verdadera.
Planteamos el sistema:
x + y + z + u + v = 1
x + y + z + u + v = 2
x + y + z = 0
u + v = 1
x +u =1
z - v = 1
Observa que si a la primera ecuación le restamos la segunda queda:
0 = -1, que es una identidad absurda, y el sistema de seis ecuaciones con cinco incógnitas que hemos planteado resulta ser incompatible.
Observa que hemos mostrado que si existe un sistema como dice la proposición, por lo que resulta ser verdadera.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 4/12/16Consideremos la función cuya expresión es: g(x) = f(x)/x, cuya derivada queda: g ' (x) = ( f ' (x)*x - f(x) ) / x2 (1).
observa, acerca de la función f:
que es continua en el intervalo I = [a,b] (porque 0 ∉ I),
que es derivable en el intervalo (a,b) (porque 0 no pertenece al intervalo abierto), y
que toma valores iguales en los extremos del intervalo cerrado, ya que: g(a) = f(a)/a = f(b)/b = g(b),
por lo que se cumplen las hipótesis del Teorema de Rolle, entonces tenemos que:
exixte y ∈ (a,b) tal que: g ' (y) = 0,
luego sustituimos la expresión señalada (1) evaluada para y, y queda:
( f ' (y)*y - f(y) ) / y2= 0, hacemos pasaje de divisor como factor y queda:
f ' (y)*y - f(y) = 0, hacemos pasaje de término y queda:
f ' (y)*y = f(y).
Espero haberte ayudado.
-
Una pregunta,cuando dice signo de f prima y signo de f prima segunda, a q se refiere? lo de extremos relativos y puntos de inflexion y demas cosas se a q se refiere ,solamente esto es q no logro entender? sera simetria cuando haces f(x)=f(-x) por ejemplo? Muchas gracias si me pueden ayudar!

Antonio Silvio Palmitano
el 4/12/16Recuerda que el signo de la derivada primera corresponde a:
intervalo de crecimiento, cuando es positivo,
intervalo de decrecimiento, cuando es negativo;
y que el signo de la derivada primera corresponde a:
intervalo de concavidad hacia arriba, cuando es positivo,
intervalo de concavidad hacia abajo cuando es negativo.
Tienes la función cuya expresión es: f(x) = (x-2)/x3, = x/x3 - 2/x3 = 1/x2 - 2/x3, cuyo dominio es: D = R - {0} = (-inf,0) u (0,+inf).
Luego planteamos sus derivadas primera y segunda:
f ' (x) = -2/x3 + 6/x4 (1),
f ' ' (x) = 6/x4 - 24/x5 (2).
Luego planteamos la condición de punto crítico (posible máximo o posible mínimo):
f ' (x) = 0, sustituimos la expresión señalada (1) y queda:
-2/x3 + 6/x4 = 0, hacemos pasaje de término y queda:
6/x4 = 2/x3, multiplicamos en ambos miembros por x4 y queda:
6 = 2x, dividimos en ambos miembros por 2 y queda:
x = 3;
luego divides al dominio en subintervalos, y en cada uno de ellos la derivada primera tendrá el mismo signo para todos sus elementos, eliges un representante en cada subintervalo, evalúas la expresión de la derivada primera, y tendrás el signo:
(-inf,0), representado por x = -1, y para él tenemos: f ' (-1) = 8 > 0, por lo que la derivada primera es positiva en este subintervalo y la función es creciente;
(0,3), representado por x = 1, y para él tenemos: f ' (1) = 4 > 0, por lo que la derivada primera es positiva en este subintervalo, y la función es creciente;
(3,+inf), representado por x = 4, y para él tenemos: f ' (4) = -1/128 < 0, por lo que la derivada primera es negativa en este subintervalo, y la función es decreciente;
observa que la función alcanza un máximo para x = 3.
Luego planteamos la condición de posible punto de inflexión;
f ' ' (x) = 0, sustituimos la expresión señalada (2) y queda:
6/x4 - 24/x5 = 0, hacemos pasaje de término y queda:
6/x4 - 24/x5 = 0, hacemos pasaje de término y queda:
6/x4 = 24/x5, multiplicamos en ambos miembros por x5 y queda:
6x = 24, dividimos por 6 en ambos miembros y queda:
x = 4;
luego divides al dominio en subintervalos, y en cada uno de ellos la derivada segunda tendrá el mismo signo para todos sus elementos, eliges un representante en cada subintervalo, evalúas la expresión de la derivada segunda, y tendrás el signo:
(-inf,0), representado por x = -1, y para él tenemos: f ' ' (-1) = 30 > 0, por lo que la derivada segunda es positiva en este subintervalo, y la función es cóncava hacia arriba;
(0,4), representado por x = 1, y para él tenemos: f ' ' (1) = -18 < 0, por lo que la derivada segunda es negativa en este intervalo, y la función es cóncava hacia abajo;
(4,+inf), representado por x = 5, y para él tenemos: f ' ' (5) = 6/3125 > 0, por lo que la derivada segunda es positiva en este intervalo, y lafunción es cóncava hacia arriba;
observa que la función tiene una inflexión para x = 4.
Espero haberte ayudado.
-
no pude encararlo.. .... se me esta complicnado aplicar.
se me ocurrio i(z-4) +2 y luego calcular su argumento, pero me queda algo en funcion z y no se que es...
sia gluien me ayuda a resolverlo.
Antonio Silvio Palmitano
el 4/12/16Tienes una transformación lineal con variable compleja:
f(z) = az + b, y para hallar el centro de giro (recuerda que es invariante para la transformación), plantea:
f(z) = z, sustituyes y queda:
az + b = z, haces pasajes de términos, extraes factor común en el primer miembro y queda:
z(a - 1) = - b, luego despejas y tienes el centro de giro:
z0 = -b/(1 - a).
Y para el ángulo de giro, debes determinar el argumento del coeficiente del término lineal en la expresión de la transformación.
En tu enunciado tienes:
a = i, b = 2 - 4i,
luego tienes para el centro de giro:
z0 = - (2 - 4i)/(1 - i), y puedes continuar el cálculo;
y para el ángulo de giro, vamos al coeficiente del término lineal:
a = i = (1)π/2 (escrito en forma polar), por lo que el ángulo de giro es: α = π/2.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 4/12/16Tomemos los dos términos del segundo miembro:
1/(s + 1) + 2/(s + 1)2 = multiplicamos y dividimos por (s + 1) en el primer término y queda:
= (s + 1)/(s + 1)2 + 2/(s + 1)2 = extraemos denominador común y queda:
= (s + 1 + 2)/(s + 1)2 = reducimos términos semejantes en el numerador y llegamos a:
= (s + 3)/(s + 1)2.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 4/12/16Veamos el argumento en el segundo límite de tu enunciado:
ax + b - ∛(6x2 - x3) = extraemos factor común x3 en el argumento de la raíz y queda:
= ax + b - ∛( x3(6/x - 1) ) = distribuimos la raíz cúbica entre los dos factores de su argumento:
= ax + b - x∛(6/x - 1) = extraemos factor común x entre el primer término y el tercer término y queda:
= ( a - ∛(6/x - 1) )x + b.
Luego, para que el límite para x tendiendo a + infinito de este argumento sea igual a cero como dice el enunciado, observa que b debe ser igual a cero, y que a debe ser igual a -1, ya que el término de la raíz tiende a -1:
Lím(x->+inf) ( ( a - ∛(6/x - 1) )x + b ) = 0, si a = -1 y b = 0.
Luego pasamos al primer límite:
Lím(x->-inf) ( (bx + d)/(ax + c) ) = reemplazamos y queda:
= Lím(x->-inf) ( d/(-x + c) ) = 0, ya que el numerador es constante y el denominador tiende a +infinito.
Espero haberte ayudado.