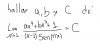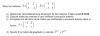-
Nicolas Ferryra
el 4/12/16Antonio Silvio Palmitano
el 4/12/16Comencemos por separar en dos factores el argumento del límite: uno racional y otro trigonométrico, y estudiemos el factor racional.
(ax4 + bx3+ 1)/(x - 1) (1)
Luego, en el numerador del primer factor, busquemos los valores de los coeficientes a y b para que 1 sea raíz doble del polinomio, y para ello empleamos dos veces la Regla de Ruffini y queda:
a b 0 0 1
1 a (a+b) (a+b) (a+b)
a (a+b) (a+b) (a+b) 1+(a+b)=0, de donde tenemos la ecuación: a + b = -1 (2)
1 a (2a+b) (3a+2b)
a (2a+b) (3a+2b) 4a+3b=0 (3);
luego resolvemos el sistema formado por las ecuaciones señaladas (2) (3), y su solución es: a = 3, b = - 4;
luego, el factor racional señalado (1) queda:
(ax4 + bx3+ 1)/(x - 1) = (3x4 - 4x3+ 1)/(x - 1) = factorizamos = (x - 1)2(3x2 + 2x + 1)/(x-1) = simplificamos = (x - 1)(3x2 + 2x + 1) (4).
Luego, tenemos para la expresión del argumento del límite:
( (ax4 + bx3 + 1)/(x - 1) ) * ( 1 / sen(πx) ) = sustituimos la expresión señalada (4):
= (x - 1)(3x2 + 2x + 1) * ( 1 / sen(πx) ) = ordenamos y asociamos factores:
= (3x2 + 2x + 1) * ( (x - 1) / sen(πx) ) (5), luego pasamos a estudiar el límite para el segundo factor (observa que el primero tiende a 6):
Lím(x->1) (x - 1) / sen(πx) =
hacemos la sustitución (cambio de variable): w = x - 1, de donde tenemos: w + 1 = x, y observa que w tiende a cero cuando x tiende a uno, sustituimos y queda:
= Lím(w->0) w /sen( π(w+1) ) = Lím(w->0) w /sen( πw+π ) = aplicamos identidad trigonométrica:
= Lím(w->0) w /(- sen(πw) ) = multiplicamos y dividimos por π:
= Lím(w->0) πw / π(- sen(πw) ) = extraemos factores constantes del denominador:
= ( 1/(-π) ) Lím(w->0) πw / sen(πw) = resolvemos (observa que tenemos un límite trascendente que seguramente has visto en clase):
= ( 1/(-π) ) * 1 = -1/π (6).
Luego, tenemos a partir de la expresión señalada (5) que el límite queda:
Lím(x->1) (3x2 + 2x + 1) * ( (x - 1) / sen(πx) ) = aplicamos la propiedad del límite de un producto:
= Lím(x->1) (3x2 + 2x + 1) * Lím(x->1) ( (x - 1) / sen(πx) ) =
resolvemos el primer factor, y reemplazamos el valor señalado (6) en el segundo factor::
= 6*(-1/π) = -6/π = C.
Espero haberte ayudado.
-
hola buenas quisiera saber si me podrian ayudar con este limite es por lhopital no se que hacer despues de ahi

David
el 5/12/16Lo que hiciste es perfecto! Ahora te toca aplicar LHOPITAL, derivando al numerador y denominador por separado...
La derivada de 1/x es -1/x²..
La derivada de (1+1/x)^x se hace por DERIVACION LOGARITMICA... Derivacion logaritmica¿Lo intentas y nos cuentas?
P.D. Determinar que el limite cuando x tiende a infinito de (1+1/x)^x es igual a "e" no requiere de demostración en tu curso y puedes decirlo inicialmente... -
Antonio Silvio Palmitano
el 4/12/16Vamos con una orientación: sabemos que el polinomio es de grado 3 y que su coeficiente principal es 2,
y que z1 = 2+i es una de sus raíces, por lo que planteamos:
P(x) = 2( x -(2+i) )(x2 + px + q) = 2(x - 2 - i)(x2 + px + q), con p y q a determinar.
Luego, planteamos:
P(1+2i) = 2(1 + 2i - 2 - i)( (1+2i)2 + p(1+2i) + q ) = 2(-1 + i)( (1+2i)2 + p(1+2i) + q ) (1),
luego, tenemos la última ecuación del enunciado:
P(1+2i) = 10(10 - 2i), sustituyes la expresión señalada (1) y queda la ecuación:
2(-1 + i)( (1+2i)2 + p(1+2i) + q ) = 10(10 - 2i), haces pasajes de factores constantes como divisores, simplificamos y queda:
(1+2i)2 + p(1+2i) + q = 5(10 - 2i)/(-1 + i), multiplicas en el segundo miembro por (-1 - i)/(-1 - i), resuelves y queda:
(1+2i)2 + p(1+2i) + q = 5(-12 - 8i)/2, resolvemos el segundo miembro y queda:
(1+2i)2 + p(1+2i) + q = - 30 - 20i, desarrollamos términos en el primer miembro y queda:
1 + 4i - 4 + p + 2pi + q = - 30 - 20i,
reducimos y agrupamos términos reales e imaginarios (suponemos que p y q son números reales) en el primer miembro y queda:
(- 3 + p + q) + (4 + 2p)i = - 30 - 20i, luego, por igualdad entre números complejos, tenemos el sistema de ecuaciones:
- 3 + p + q = -30
4 + 2p = - 20, de donde despejamos y queda: p = -12,
luego reemplazamos en la primera ecuación y queda. q = -15.
Por lo tanto, la expresión del polinomio queda:
P(x) = 2(x - 2 - i)(x2 - 12x -15).
Espero haberte ayudado.
-
considerando las matrices siguientes A= 1 -2 B= 2 -1 C= 3 -12
0 1 1 1 0 5
calcula X para que se cumpla A² . X -B =C ayuda resolviendo este ejercicio :(
-
Por favor ayudadme con este ejercicio, mañana tengo examen, muchas gracias de antemano :D.

David
el 5/12/16SUSTITUYE X POR 1 en el primer trozo e iguala a 1... Obtendrás una ecuación..
Intenta hacer el limite por la izquierda y por la derecha e igualalos (para que se a continua)....
Tendrás otra ecuacion. Resuelve el sistema...
Te sugiero los vídeos de "discontinuidad en una funcion a trozos" -
Hola, haciendo los ejercicios resueltos de matrices me he encontrado con que el ejercicio 3 está mal. El enunciado pone tenemos que hallar la x para que A2 - xA + yI = 0 y en la solución pone: Calculamos A2 - xA - yI e igualamos a 0 por lo que todo el ejercicio está mal.
-
 Me gustaría saber por qué al factorizar esta fracción se cambia de signo la primera x del numerador y todo el denominador, gracias!!
Me gustaría saber por qué al factorizar esta fracción se cambia de signo la primera x del numerador y todo el denominador, gracias!!Lucía
el 4/12/16Ángel
el 4/12/16Se multiplicó por "menos" en el numerador y en el denominador para que el denominador quedara como lo de dentro del paréntesis, para despejar
Se utilizó como estrategia, pero ten en cuenta que no alteró la ecuación (pues menos entre menos es más, que es lo que teníamos en principio)