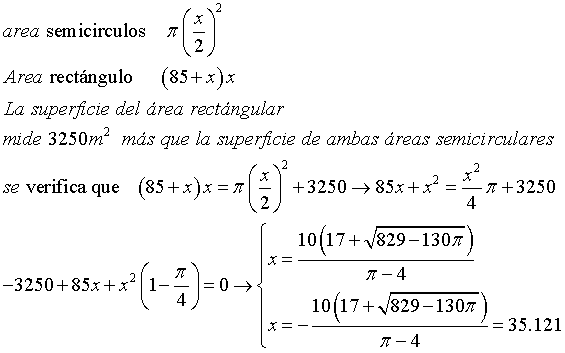-
hola
alguien podría ayudarme con esto ?
Es posible encontrar números enteros m y p de modo que se verifiquen las siguientes relaciones? ¿Cuántos hay? ¿Por qué?
a) m · p · m < 0, con p < 0
b) m · p · m · p < 0, con p < 0
c) m · p · m · p · m < 0, con p < 0
gracias
Jose Ramos
el 21/8/19a) Se verifica para todo número p<0, pues m.p.m = m2 p. m2 >0 para todo número real distinto de cero y p <0, entonces m.p.m = m2 p < 0 (CIERTO PARA TODO p > 0 y m cualquier valor no nulo)
b) Nunca se verifica, es decir que no es posible puesto que m · p · m · p = m2 .p2 = (mp)2 que en ningún caso es < 0 (NO ES POSIBLE)
c) Se verifica cuando m > 0 , pues m · p · m · p · m = m3 .p . Si m <0, como p <0 entonces m3 .p > 0. Si m >0, como p <0 entonces m3 .p <0 (CIERTO para todo m > 0 y todo p < 0)
-
Hola necesito que me aclaren algo así no me confundo. Si la Formula del semicírculo y semicircunferencia es π×r² ⁄ 2 y cuando está completa es π×d² ⁄4, la pregunta es cual de las dos fórmulas utilizo si me piden hallar el diámetro del semicírculo o semicircunferencia sola, eso es todo, espero que me entiendan gracias.
-
Tengo la función f(x) = e-3x . La derivada me dio F'(x) = -3e-3x Luego, lo iguale a 0, porque debo hallar sus extremos, aqui es cuando no estoy segura de que hacer. Comencé a hacer el signo de la derivada, e elevado a cualquier cosa tiene que ser mayor que 0, así que sustituí 1 y -1 en la derivada, ambos valores me dieron negativo... que debo hacer?
Antonius Benedictus
el 20/8/19Jose Ramos
el 21/8/19 -
Un trozo de madera de 1,2 m de largo tiene forma de un tronco de cono circular de diámetro 40 cm y (40+ h) cm en sus bases, donde h ≥ 0 es conocido. Determinar en función de h, el mayor volumen del cilindro circular recto que se pude cortar de este trozo de madera, de modo que su eje coincida con el del tronco del cono. No he podido con este ejercicio? podrían ayudarme?
-
Hola quería saber como resuelvo este problema, lo eh tratado de resolver pero nunca llego a una respuesta aceptable, desde ya agradezco la ayuda,gracias.
El terreno de un campo de deportes está constituido por un área rectangular cuyo largo mide 85m más
que el ancho y por dos áreas semicirculares ubicadas a ambos lados del área rectángular, de modo que
el diámetro es coincidente y de igual medida que el ancho del rectángulo. La superficie del área rectángular
mide 3250m cuadrado más que la superficie de ambas áreas semicirculares. Entonces el ancho y el largo miden.
Expresar el resultado sin decimales.
Antonio Silvio Palmitano
el 20/8/19Puedes designar con x al largo del sector rectangular, y con y a su ancho.
Luego, puedes plantear la ecuación:
x = y + 85 (1) (en metros) ("el largo es 85 metros más que el ancho").
Luego, planteas la expresión del área del sector rectangular, y queda:
Ar = x*y (2).
Luego, planteas la expresión del área total de los dos sectores semicirculares (observa que tienes un círculo completo), y queda:
Ac = π*y2/4 (3) (en m).
Luego, puedes plantear la ecuación:
Ar = Ac + 3250 (4) (en m2) ("el área rectangular mide 3250 m2 más que el área de los dos sectores semicirculares juntos").
Luego, sustituyes las expresiones señaladas (2) (3) en la ecuación señalada (4), y queda:
x*y = π*y2/4 + 3250;
luego, sustituyes la expresión señalada (1) en el primer miembro, y queda:
(y+85)*y = π*y2/4 + 3250, distribuyes el primer miembro, y queda:
y2 + 85*y = π*y2/4 + 3250, multiplicas por 4 en todos los términos, y queda:
4*y2 + 340*y = π*y2 + 13000, restas π*y2 y restas 13000 en ambos miembros, y queda:
4*y2 + 340*y - π*y2 - 13000 = 0, extraes factor común entre los términos cuadráticos, y queda:
(4 - π)*y2 + 340*y - 13000 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
1°)
y = ( -340 - √( 3402 + 52000*(4 - π) ) )/( 2*(4 - π) ) ≅ -431,203 m,
que no tiene sentido para este problema (recuerda que y es el ancho del sector rectangular, por lo que debe ser positivo);
2°)
y = ( -340 + √( 3402 + 52000*(4 - π) ) )/( 2*(4 - π) ), resuelves, y queda: y ≅ 35,121 m;
luego, reemplazas este valor remarcado en la ecuación señalada (1), y queda:
x ≅ 35,121 + 85, resuelves, y queda: x ≅ 120,121 m.
Espero haberte ayudado.
-
Antonius Benedictus
el 20/8/19Jose Ramos
el 20/8/19 -
El 20% de una cantidad es 30. ¿Cuál esdicha cantidad? que tengo que hacer para tener el resultado
Jose Ramos
el 20/8/19Si no lo quieres plantear como una regla de tres, puedes hacerlo con una ecuación de 1º grado muy simple: Llamas x a la cantidad que buscas y como el 20% de x es 20x/100, la ecuación que obtienes es:
20x/100 = 30, entonces la resuelves 20x = 3000 x = 3000/20 = 150