-
-
Jose Ramos
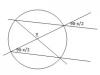
el 19/8/19Le llamas a al ángulo en C que es igual al ángulo en B en el ΔABD según el enunciado. Como los triángulos ABC y DBE son iguales, el ángulo en E es también a. Llamas b al ángulo B en el triangulo DBF y llamas c al ángulo B en el triángulo FBE, entonces por la igualdad de triángulos del enunciado, a+b=b+c, de donde a = c. Esto quiere decir que el triángulo BFE es isósceles porque el ángulo en E y en B vale a, entonces el ángulo en F es 180-2a.
Vamos ahora al triángulo CFD. El ángulo F en 180-2a por ser opuesto por el vértice al triángulo BFE. Como el ángulo C era a, el ángulo en D es a. Hemos demostrado que el triángulo CFD tiene dos ángulos iguales, por lo tanto ES ISÓSCELES.
-
Una bandeja de evaporación tiene un diametro de 120 cm y una profundidad de 25 cm.
Calcular el area superficial de la bandeja de en m2
Si el volumen inicial de agua la bandeja es de 44 litros, cual es la profundidad en mm?
Ayuda por favor, gracias.
-
Jose Ramos
el 19/8/19DG = GB es cierta. La que es falsa es AD = DB (Lo he comprobado gráficamente en Geogebra)
El triángulo ADB es rectángulo en D y el BOG es rectángulo en G. Como B es un vértice común a ambos rectángulos resulta que los dos triángulos son semejantes, es decir que DB/GB = DA/OG = AB/OB = 2r/r =2. Tenemos que DB = 2GB y DA = 2OG.
Si AD fuese igual a DB, 1=AD/DB = OG/GB, entonces OG = GB lo que es falso, por tanto AD y DB no son iguales.
-
Jose Ramos
el 19/8/19La demostración se hace basándose en que los triángulos EOB y AOD son isósceles, pues sus ángulos en O son opuestos por el vértice y son el mismo ángulo (x), y los otros miden 90-(x/2) en ambos. Prolongando obtenemos la figura siguiente, donde queda demostrado el paralelismo
-
Hola amigos,
Soy nuevo en este foro que me parece magnífico. Tengo un problema: A veces respondo alguna duda que plantean los visitantes al foro que ya ha sido respondida correctamente por algún otro compañero/profesor, pero yo no la veo hasta después de haber dado al botón "responder". Esto tiene dos inconvenientes: 1º) El trabajo que me paso resolviendo el problema es una pérdida de tiempo, porque ya ha sido resuelto por otro. 2º) Pareciera que estoy interfiriendo en el trabajo de otro compañero.
Me he percatado recientemente de que tengo la posibilidad de eliminar el post, con lo cual soluciono el problema 2º, pero me pregunto si vosotros podeís resolver el problema 1º), es decir como saber que la pregunta ya ha sido respondida y ver dicha respuesta de inmediato antes de acometer una solución que ya ha sido enviada.
Gracias y un saludo a todos. Realizáis (amos) un fenomenal trabajo.
Jose
el 19/8/19La unica forma seria actualizando la pagina constantemente, porque el 1er problema que te ocurre es porque tu y otra persona estan desarrollando el problema al mismo tiempo y la otra persona lo sube unos minutos o segundos antes de que tu termines ,y a ti todavia no te aparece resuelto ,por que no has actualizado la pagina.
Antonio Silvio Palmitano
el 19/8/19 -
si se quiere vallar un campo rectangular que está junto a un camino. Si la valla del lado del camino cuesta 80 Euros/ y la de los otros 10 Euros/ m , halla el área de mayor campo que puede cercarse con 28800 euros. Podrían ayudarme con este ejercicio ??