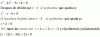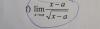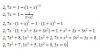-
como puedo saber si dos rectas son paralelas dados los angulos'
Antonio Silvio Palmitano
el 30/4/19 -
Saludos, me podrían facilitar un Link donde pueda descargar el libro matemática básica 2 de Saal, gracias
César
el 30/4/19 -
cuánto da -2÷3•(-1) ????
Antonio Silvio Palmitano
el 29/4/19Veamos.
Observa que la expresión a resolver consta de un único término.
Luego, si tienes el caso:
[ -2/3 ]*(-1) = resuelves la multiplicación = 2/3.
O, si tienes el caso:
-2/[ 3*(-1) ] = resuelves el denominador = -2/(-3) = resuelves signos = 2/3.
O sea, el resultado es 2/3.
Espero haberte ayudado.
-
Hola alguien me pude ayudar con esto?
a)Escribe la ecuación de la recta,r, que pasa por los puntos (1,2) i (2,-1)
b)Obten la ecuación de la recta,s, que pasa por(1,-3) i tiene pendiente 2
c)Encuentra el punto de corte de las dos rectas anteriores
-
 hola me pueden ayudar en este ejercicio? Se hacer lo demás pero cuando viene lo de (x-1)(x-3)(x+2) no sé de donde sale, me pueden ayudar a como sacarlo por favor
hola me pueden ayudar en este ejercicio? Se hacer lo demás pero cuando viene lo de (x-1)(x-3)(x+2) no sé de donde sale, me pueden ayudar a como sacarlo por favordAmian
el 29/4/19Antonio Silvio Palmitano
el 29/4/19Aquí debes inspeccionar, y observa que x = 1 es una solución de la ecuación de tu enunciado, ya que se cumple la identidad:
13 - 2*12 - 5*1 + 6 = 1 - 2 - 5 + 6 = 0;
Luego, divides al polinomio de tu enunciado por (x-1) (recuerda que las raíces se ven a simple vista con sus signo cambiado en sus factores correspondientes), y tienes la factorización parcial:
x3 - 2*x2 - 5*x + 6 = (x-1)*(x2-x-6) (1).
Luego, puedes plantear la condición para las raíces del segundo factor:
x2 - x - 6 = 0, que es una ecuación polinómica cuadrática, cuyas soluciones son:
x = -2, a la que le corresponde el factor: (x+2),
x = 3, a la que le corresponde el factor: (x-3).
Luego, sustituyes los dos últimos factores remarcados en lugar del segundo factor de la expresión señalada (1), y queda (observa que el coeficiente principal del polinomio de tu enunciado es 1):
x3 - 2*x2 - 5*x + 6 = (x-1)*(x+2)*(x-3).
Espero haberte ayudado.
-
Marcos
el 29/4/19Antonio Silvio Palmitano
el 29/4/19d)
Vamos con otra opción.
Distribuyes la raíz cuadrada en el segundo factor, resuelves para el numerador, y queda:
Lím(x→+∞) (x2 + 3x + 2) * ( 1/√(x + 3) ) =
resuelves la multiplicación de expresiones, y queda:
= Lím(x→+∞) (x2 + 3x + 2) / √(x + 3) =
extraes factor común (x2) en el numerador, extraes factor común (x) en el argumento de la raíz, simplificas expresiones, y queda:
= Lím(x→+∞) x2*(1 + 3/x + 2/x2) / √( x*(1 + 3/x) ) =
distribuyes la raíz en el denominador, expresas al primer factor del denominador en forma de potencia, y queda:
= Lím(x→+∞) x2*(1 + 3/x + 2/x2) / x1/2*√(1 + 3/x) =
simplificas las potencias con bases iguales, y queda:
= Lím(x→+∞) x3/2*(1 + 3/x + 2/x2) / √(1 + 3/x) = +∞ (o tiende a +infinito, como indica el colega Marcos),
porque observa que el primer factor del numerador tiende a +infinito, el segundo factor del denominador tiende a 1, y el denominador tiende a uno.
Espero haberte ayudado.
Antonio Omg
el 29/4/19Antonio Omg
el 29/4/19Antonio Silvio Palmitano
el 29/4/19c)
Tienes la expresión de la base de la potencia del argumento del límite de tu enunciado:
f(x) = (x-1)/(2x-5), efectúas la división del numerador entre el denominador, y queda:
f(x) = 1/2 + (3/2)/(2x-5), extraes factor común (1/2), y queda:
f(x) = (1/2)*( 1 + 3/(2x-5) ),
divides por 3 en el numerador y en el denominador del segundo término del agrupamiento, y queda:
f(x) = (1/2)*( 1 + 1/( (2x-5)/3 ) ) (1),
y observa que el denominador del segundo término tiende a +infinito.
Tienes la expresión del exponente de la potencia del argumento del límite de tu enunciado:
n(x) = x+5, multiplicas por (2x-5)/3 y por 3/(2x-5), y queda:
n(x) = (2x-5)/3 * (x+5)*3/(2x-5), resuelves la multiplicación de los dos últimos factores, y queda:
n(x) = (2x-5)/3 * (3x+15)/(2x-5), resuelves la división en el segundo factor, y queda:
n(x) = (2x-5)/3 * ( 3/2 + (45/2)/(2x-5) ) (2),
y observa que el segundo término de esta expresión tiende a cero.
Luego, planteas la expresión del argumento de tu límite:
A(x) = ( (x-1)/(2x-5) )x+5,
sustituyes la expresión señalada (1) en lugar de la base, y queda:
A(x) = ( (1/2)*( 1 + 1/( (2x-5)/3 ) ) )x+5,
distribuyes el exponente entre los dos factores de la base de la potencia, y queda:
A(x) = (1/2)x+5 * ( 1 + 1/( (2x-5)/3 ) )x+5,
distribuyes el exponente del primer factor entre su numerador y su denominador, resuelves su numerador, y queda:
A(x) = 1/2x+5 * ( 1 + 1/( (2x-5)/3 ) )x+5,
y observa que el denominador del primer factor tiende a +infinito, por lo que tienes que el primer factor tiende a cero por la derecha;
luego, sustituyes la expresión señalada (2) en lugar del exponente de la potencia en el segundo factor, y queda:
A(x) = 1/2x+5 * ( 1 + 1/( (2x-5)/3 ) )(2x-5)/3 * ( 3/2 + (45/2)/(2x-5) ),
aplicas la propiedad de una potencia cuya base es otra potencia en el segundo factor, y queda:
A(x) = 1/2x+5 * [ ( 1 + 1/( (2x-5)/3 ) )(2x-5)/3 ]( 3/2 + (45/2)/(2x-5) ) (3).
Luego, observa que la expresión encerrada entre corchetes tiende a e (base de los logaritmos naturales), observa que el exponente tiende a 3/2, y que el primer factor tiende a cero, por lo que puedes concluir que el límite de la expresión de tu enunciado para x tendiendo a +infinito es:
L = 0*e3/2= 0.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 29/4/19c)
Otra forma.
Planteas la expresión del logaritmo natural del límite de tu enunciado, y queda:
ln(L) = (x+5) * ln[ (x-1)/(2x-5) ],
resuelves la división del argumento del logaritmo (observa que ya la hemos hecho en la entrada anterior), y queda:
ln(L) = (x+5) * ln[ 1/2 + (5/2)*( 1/(2x-5) ) ] (1).
Luego, observa que el primer factor de esta expresión tiende a +infinito, y observa que el segundo factor tiende a ln(1/2) que es un número negativo, por lo que tienes que el logaritmo del límite tiende a -infinito, por lo que puedes concluir que el límite de la expresión de tu enunciado des 0.
Espero haberte ayudado.
-
me gustaria saber que es lo que hay que hacer para que alguien te heche una mano con un ejercicio.
hay que seguir alguna clase de instrucciones, hay que pagar quisiera saberlo para tenerlo en cuenta.
-
Alguien me puede resolver esta ecuación:
-3
2,7x = 1 - (1 + x)
Esta elevado a -3 el (1+x)
No consigo despejar ni aplicando logaritmos. El resultado la variable lo se pero lo que me interesa es la forma de resolver la ecuación.
Antonio Silvio Palmitano
el 29/4/19Continuamos con el desarrollo que propone el colega David.
Extraes factor común en la primer miembro, y queda:
x*(2,7x3 + 7,1x2 + 5,1x - 0,3) = 0;
luego, por anulación de una multiplicación tienes dos opciones:
1°)
x = 0, que es una solución válida de la ecuación de tu enunciado;
2°)
2,7x3 + 7,1x2 + 5,1x - 0,3 = 0, multiplicas por 10 en todos los términos, y queda:
27x3 + 71x2 + 51x - 3 = 0,
que es una ecuación polinómica cúbica, que puedes resolver por medio de la Fórmula de Cardano, y observa que tienes a tu disposición un vídeo aquí en Unicoos que puede serte útil para aplicarla, y a partir de ella obtendrás las tres soluciones distintas de cero que te muestra el colega César.
Espero haberte ayudado.