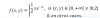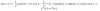-
Antonio Sanchez
el 26/4/19
hola buenas, podeis decirme si tengo bien esta derivada? -
Silvia Alonso Toledano
el 26/4/19 -
magui
el 26/4/19 -
Mrcarlos007
el 26/4/19 -
Uriel Dominguez
el 26/4/19 -
Jose
el 26/4/19 -
Breogan Alvarez Ballesteros
el 26/4/19Veamos, si tenemos un suceso A que tiene un 20% de probabilidad cada 1'7s de provocar un efecto, y otro suceso B que tiene un 15% de probabilidad cada 1s de provocar otro suceso, ambos totalmente independientes, pero sucediendo al mismo tiempo, como calculo la probabilidad de que ambos efectos de los dos sucesos independientes ocurran a la vez? gracias
David
el 26/6/19Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
magui
el 26/4/19
Buenas noches, me ayudarian con el ítem C ? No entiendo muy bien que seria contener al eje de abscisas (X) el punto sería (X, 0,0)? Gracias -
micaela
el 26/4/19
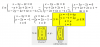
Hola mi duda es la siguiente, respecto al ejercicio 16 para calcular el volumen del solido de revolucion alrededor del eje x deberia usar el metodo de los cascarones cilindricos debido a que parte desde x=2 o usar el metodo de los discos. Y ademas queria saber si el metodo de los cascarones se puede utilizar tambien con una rotacion sobre el eje y. Nose si mi pregunta es muy extensa agradeceria cualquier respuesta gracias
-
Manuel Perez
el 25/4/19Estudiar su derivabilidad. Que hago mal??
3x2-5x si x<-1 3x2-5x-8/x+1= 0/0 indeterminación
2x2 si x≥-1
Antonio Silvio Palmitano
el 26/4/19Si tienes la expresión de una función en dos trozos:
f(x) =
3x2-5x si x < -1,
2x2 si x ≥ -1.
Luego, observa que las expresiones de los trozos son derivables, por lo que la expresión de la función derivada queda:
f ' (x) =
6x-5 si x < -1,
a determinar si x = 1,
4x si x > -1;
luego, solo queda calcular las derivadas laterales por medio de la definición en el punto de corte entre los trozos, observa que el valor de la función en este punto en estudio es: f(-1) = 2(-1)2 = 2, y tienes:
f-' (-1) =
= Lím(x→-1-) ( f(x) - f(-1) )/( x-(-1) ) =
= Lím(x→-1-) ( 3x2-5x - 2 )/( x+1 ) = -∞,
porque puedes observar que el numerador tiende a 6 y que el denominador tiende a cero desde valores negativos;
y como esta derivada lateral no existe, ya puedes afirmar que la función derivada no está definida en x = -1, y no es necesario que plantees la derivada lateral por la derecha.
Por lo tanto, la expresión de la función derivada queda:
f ' (x) =
6x-5 si x < -1,
no está definida si x = 1,
4x si x > -1.
Espero haberte ayudado.
