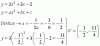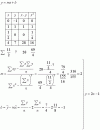
Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Jose
el 25/4/19

Hola buenas noches, me ayudais con este ejercicio?

••0 voto/s
•
César
el 25/4/19

•0 voto/s
•

Cancelar
Bet
el 24/4/19

Ayuda porfavor

••0 voto/s
•
Antonius Benedictus
el 24/4/19
Las tres primeras cumplen todos los axiomas.
La cuarta puede dar lugar a distancias negativas. No vale.

•0 voto/s
•

Cancelar
María
el 24/4/19

Buenas. ¿Alguien sabe cómo puedo justificar la construcción de un paralelepípedo a partir de sus tetraedros? Es decir, cómo se pueden saber las medidas de estos tetraedros.

••0 voto/s
•
Antonius Benedictus
el 24/4/19

•0 voto/s
•

Cancelar
Ivan Gijon Arruabarrena
el 24/4/19

¿Alguien me podría ayudar? Primero realizo la tabla y luego he hecho los calculos pero la media me sale negativa y no se si estara bien o mal. Gracias de ante mano.

••0 voto/s
•
Antonius Benedictus
el 24/4/19
Puede serlo (esperanza de perder en un juego):

•0 voto/s
•

Cancelar
irene braza mera
el 24/4/19

Cuanto da -(-1)^2+1

••0 voto/s
•
Antonio Silvio Palmitano
el 24/4/19
Recuerda: (-1)² = 1, por lo que tienes: -(-1)² = -1.
Luego, tienes la expresión:
-(-1)² + 1 = reemplazas = -1 + 1 = cancelas términos opuestos = 0.
Espero haberte ayudado.

•0 voto/s
•
Francisco Javier Tinoco Tey
el 24/4/19
Da cero, utiliza siempre los siguientes pasos:
1) Paréntesis y corchetes
2) Potencias y radicales
3) Sumas y restas de izquierda a derecha
-(-1)²+1=-1+1=0
Espero haberte ayudado, un saludo. Javi Tinoco

•0 voto/s
•

Cancelar
RODRIGO
el 24/4/19

No consigo que en el ejercicio 9 me salga representada una parábola ni de broma. Ayudaaaa

••0 voto/s
•
César
el 24/4/19

•0 voto/s
•

Cancelar
Shany sosa
el 24/4/19

Hola me pueden ayudar con el enunciado número 15, no se de donde sale esa respuesta que me dan, ya que, al realizar las cuentas me da menos

••0 voto/s
•
Breaking Vlad
el 6/6/19
Hola,
si pudieras poner lo que has hecho podríamos ayudarte mejor.

•0 voto/s
•

Cancelar
Jose
el 24/4/19

Buenas tardes, alguien sabría como hacer esto? me tiene la cabeza loca :(

••0 voto/s
•
Antonius Benedictus
el 24/4/19
Diagonaliza la matriz. Te queda A=P·D·P^-1
A^5 =(PDP^-1)·(PDP^-1)·(PDP^-1)·(PDP^-1)·(PDP^-1)=P·D^5·P^-1=P· ·P^-1 =

•0 voto/s
•

Cancelar
Mauro
el 24/4/19

El ejercicio de Ecuaciones Diferenciales dice asi, y'' + 4y = 0 , y= C₁sen (2x) + C₂cos (2x)

Alguien lo sabe resolver?

••0 voto/s
•
Antonio Silvio Palmitano
el 24/4/19
Tienes la ecuación diferencial lineal, de segundo orden con coeficientes constantes y homogénea:
y '' + 4y = 0, cuya ecuación característica es:
r² + 4 = 0, cuyas soluciones son los números complejos: r₁ = 2i y r₂ = -2i.
Luego, tienes que su solución general tiene la expresión explícita:
y = C₁*sen(2x) + C₂*cos(2x) (1), con C₁ ∈ R y C₂ ∈ R.
Luego, a fin de verificar la validez de la solución general que tienes remarcada, planteas las expresiones de sus derivadas primera y segunda, y queda:
y ' = 2*C₁*cos(2x) - 2*C₂*sen(2x),
y '' = -4*C₁*sen(2x) - 4*C₂*cos(2x) (2);
luego, planteas la expresión del primer miembro de la ecuación diferencial que tienes en tu enunciado, y queda:
y '' + 4y =
sustituyes la expresión señalada (2) en el primer término, sustituyes la expresión señalada (1) en el segundo factor del segundo término, y queda:
= -4*C₁*sen(2x) - 4*C₂*cos(2x) + 4( C₁*sen(2x) + C₂*cos(2x) ) =
distribuyes el tercer término, y queda:
= -4*C₁*sen(2x) - 4*C₂*cos(2x) + 4*C₁*sen(2x) + 4*C₂*cos(2x) =
cancelas términos opuestos, y queda:
= 0.
Espero haberte ayudado.

•1 voto/s
•

Cancelar