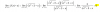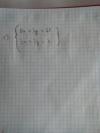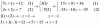-
Antonio Silvio Palmitano
el 31/3/19Tienes tres secciones que conforman el sólido, por lo que puedes plantear que su volumen es igual a la suma de los volúmenes de las secciones:
1)
Cilindro circular recto, cuyo radio mide 10 cm y cuya altura mide 15 cm, por lo que tienes:
V1 = π*R2*h1 = π*102*15 = 1500*π cm3.
2)
Prisma rectángular recto, cuyo ancho y cuyo largo miden 20 cm (dos radios del cilindro anterior), y cuya altura mide 10 cm, por lo que tienes:
V2 = a*L*h = 20*20*10 = 4000 cm3.
3)
Cono circular recto, cuyo radio de base mide 10 cm (coincide con el radio del cilindro), y cuya generatriz mide 26 cm;
luego, planteas la expresión de la longitud de la altura del cono en función del radio de su base y de la generatriz, y queda:
h3 = √(g2 - R2) (1);
luego, plantes la expresión del volumen del cono en función del radio de su base y de su altura, y queda:
V3 = (1/3)*π*R2*h, sustituyes la expresión señalada (1), y queda:
V3 = (1/3)*π*R2*√(g2 - R2) = (1/3)*π*102*√(262 - 102) = (1/3)*π*100*18 = 600*π cm3.
Luego, tienes para el volumen total del sólido:
V = V1 + V2 + V3 = 1500*π + 4000 + 600*π = (4000 + 2100*π) cm3 ≅ 10597,345 cm3.
Espero haberte ayudado.
-
Buenas me pueden ayudar con este problema
¿A que velocidad tengo que ir para dar una vuelta de 13 kilómetro en 29 minutos?
Antonio Silvio Palmitano
el 31/3/19Tienes el valor del desplazamiento: Δx = 13 Km = 13000 m.
Tienes el valor del intervalo de tiempo empleado: Δt = 29 min = 29*60 = 1740 s.
Luego, planteas la expresión de la velocidad media, y queda:
vm = Δx/Δt, reemplazas valores, resuelves, y queda:
vm ≅ 7,471 m/s, cuyo valor en Km/h queda:
vm ≅ 7,471*3600/1000 ≅ 26,897 Km/h.
Espero haberte ayudado.
-
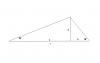
si alguien puede responderme: dos personas, separadas entre si cierta distancia, ven a un avion que vuela a 1800 m de altura, situado entre ambas y en su mismo plano vertical, con ángulos de 70º y 35º, respectivamente. ¿A que distancia está cada persona de la otra ?
Antonio Silvio Palmitano
el 31/3/19Observa la figura, en la que hemos llamado x a la distancia entre las personas, y hemos llamado h a la altura del avión con respecto al suelo.
Luego, observa que tienes dos triángulos rectángulos, cuyas bases hemos llamado a y b.
Luego, observa que puedes plantear las ecuaciones:
x = a + b (1),
tan(35°) = h/a, de aquí despejas: a = h/tan(35°) (2),
tan(70°) = h/b, de aquí despejas: b = h/tan(70°) (3);
luego, sustituyes las expresiones señaladas (2) (3) en la ecuación señalada (1), y queda:
x = h/tan(35°) + h/tan(70°),
extraes factor común, y queda:
x = h*( 1/tan(35°) + 1/tan(70°) ).
aquí reemplazas el valor de la altura, resuelves, y queda:
x ≅ 3225,813 m.
Espero haberte ayudado.
-
Actividad 8: Después de realizar varios sondeos sobre una población con problemas socioeconómicos, se ha conseguido averiguar que únicamente un 15% de la misma es favorable a los tratamientos de psicoterapia. Elegida una muestra de 50 personas de dicha población, calcula:
a) La probabilidad de que haya más de cinco personas favorables a dichos tratamientos.
b) La probabilidad de que, a lo sumo, haya seis personas favorables a los tratamientos.
-
Actividad 7: Se sabe, por una estadística sociológica realizada recientemente, que el nivel de aceptación de un determinado partido político es del 25% de la población. De una muestra aleatoria de 40 personas, se desea saber cuál es la probabilidad de que 15 de ellas acepten a dicho partido. Halla esta probabilidad.
-
Hola, me podrían ayudar con ese ejercicio? Es por sumas de Riemann, lo intento hacer así porque así nos lo piden en clase, hice eso pero creo está mal... He visto que hay una resolución un poco más corta y aplicando esa, si me sale... Espero puedan ayudarme

Antonio Silvio Palmitano
el 31/3/19Vamos con una orientación.
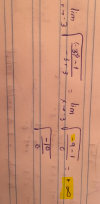
Tienes el intervalo: [1,3], lo divides en n intervalos, y la longitud de cada intervalo es: h = 2/n.
Luego, planteas la expresión de la función: f(x) = 2*x-1 para algunos de los primeros valores que limitan subintervalos, y tienes:
f(1) = f(1+0*2/n) = 2*(1+0*2/n)-1 = 2+0/n-1 = 1+0/n = 1+4*0/n,
f(1+1*2/n) = 2*(1+1*2/n)-1 = 2+4/n-1 = 1+4/n = 1+4*1/n,
f(1+2*2/n) = 2*(1+2*2/n)-1 = 2+8/n-1 = 1+8/n = 1+4*2/n,
f(1+3*2/n) = 2*(1+3*2/n)-1 = 2+12/n-1 = 1+12/n = 1+4*3/n,
y observa que en general tienes la expresión:
f(1+k*2/n) = 2*(1+k*2/n)-1 = 2+4*k/n-1 = 1+4*k/n,
y para el valor extremo derecho del intervalo tienes:
f(3) = f(1+n*2/n) = 2*(1+n*2/n)-1 = 2 + 4*n/n-1 = 1+4n/n = 1+4 = 5.
Luego, te mostramos dos opciones:
1°)
Si tomas los valores "izquierdos" para cada subintervalo, tienes la Suma de Riemann:
Si =
= ∑(k=0,n-1) f(1+4*k/n)*h = sustituyes expresiones remarcadas, y queda:
= ∑(k=0,n-1) (1+4*k/n)*(2/n) = distribuyes en el argumento de la sumatoria, y queda:
= ∑(k=0,n-1) (2/n+8*k/n2) = aplicas la propiedad de la suma de sumatorias, y queda:
= ∑(k=0,n-1) (2/n) + ∑(k=0,n-1) (8*k/n2) = extraes factores independientes del índice (k) en ambas sumatorias, y queda:
= (2/n)*∑(k=0,n-1) (1) + (8/n2)*∑(k=0,n-1) (k) = resuelves ambas sumatorias remarcadas, y queda:
= (2/n)*(n) + (8/n2)*(n*(n-1)/2) =
simplificas en el primer término, distribuyes y simplificas en el segundo término, y queda:
= 2 + 4 - 4/n = reduces términos semejantes, y queda:
= 6 - 4/n;
luego, tomas el límite para n tendiendo a infinito, y queda:
Lím(n→∞) Si = Lím(n→∞) (6 - 4/n) = 6 - 0 = 6.
2°)
Si tomas los valores "derechos" para cada subintervalo, tienes la Suma de Riemann:
Sd =
= ∑(k=1,n) f(1+4*k/n)*h = sustituyes expresiones remarcadas, y queda:
= ∑(k=1,n) (1+4*k/n)*(2/n) = distribuyes en el argumento de la sumatoria, y queda:
= ∑(k=1,n) (2/n+8*k/n2) = aplicas la propiedad de la suma de sumatorias, y queda:
= ∑(k=0,n) (2/n) + ∑(k=0,n-1) (8*k/n2) = extraes factores independientes del índice (k) en ambas sumatorias, y queda:
= (2/n)*∑(k=1,n) (1) + (8/n2)*∑(k=1,n) (k) = resuelves ambas sumatorias remarcadas, y queda:
= (2/n)*(n) + (8/n2)*(n*(n+1)/2) =
simplificas en el primer término, distribuyes y simplificas en el segundo término, y queda:
= 2 + 4 + 4/n = reduces términos semejantes, y queda:
= 6 + 4/n;
luego, tomas el límite para n tendiendo a infinito, y queda:
Lím(n→∞) Sd = Lím(n→∞) (6 + 4/n) = 6 + 0 = 6.
Y puedes luego verificar la validez de los resultados obtenidos con la resolución de la integral por medio de los métodos que has visto en clase.
Espero haberte ayudado.
-
Antonio
el 31/3/19