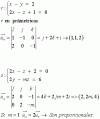-
Elena
el 5/2/19Hola me podríais ayudar con este ejercicio:
Se consideran las rectas:
r : x − y = 2 s: 2x - z + 2 = 0
2x − z + 1 = 0 2y - mz = 6
a) Hallar el valor de m para que r y s sean paralelas.
Lo que nose es como pasar la recta s a forma implícita para saber el vector director y el punto
Antonio
el 5/2/19 -
Fernando
el 5/2/19Teniendo el plano π: 2x+ay+4z+25=0 y la recta r: x+1=(y-1)÷2=(z+3)÷5.
a) Consigue el valor del parámetro a para que r esté en el plano π.
b) Para el valor a=-2, consigue uno o varios puntos que se encuentren dentro de la recta que pasa por el punto P(-3/2, 0, -11/2) y sea perpendicular al plano π. Sabiendo que se encuentra o encuentran a una distancia de √6u.
c) Para el valor de a=-2, consigue el ángulo que forman la recta r y el plano π.
-
Fernando
el 5/2/19Teniendo los siguientes puntos: A(0,0,1), B(1,0,-1), C(0,1,-2), D(1,2,0).
a) Son coplanarios?
b) Consigue la ecuación del plano π que forman los puntos A,B y C.
c) Consigue la distancia del punto D al plano π.
-
Susana Rubio Blazquez
el 5/2/19 -
Quiroga
el 5/2/19Hola buenas, no se como seguir con este problema, he calculado esto:
ç
1. ¿Para qué valores n e N el siguiente numero complejo es real?
Antonio Silvio Palmitano
el 5/2/19Vas muy bien.
Luego, para que la expresión sea real, debes plantear que la parte imaginaria es igual a cero, y tienes la ecuación:
sen(n*π/2 - π/2) = 0, compones en ambos miembros con la función inversa del seno, y queda:
n*π/2 - π/2 = k*π, con k ∈ N;
luego multiplicas por 2 y divides por π en todos los términos de la ecuación, y queda:
n - 1 = 2*k, con k ∈ N,
sumas 1 en ambos miembros de la ecuación, y queda:
n = 2*k + 1, con k ∈ N,
por lo que puedes concluir que n debe ser un número natural impar.
Espero haberte ayudado.
-
milagroscumbrerass
el 5/2/19
Alguien me puede resolver la actividad 3 y 5. Gracias. Por favor
Antonio Silvio Palmitano
el 5/2/19Tienes el número complejo:
z = 1/3 + 4*i,
cuyo conjugado es:
zc = 1/3 - 4*i.
Luego, planteas la expresión del cuadrado de la suma del número complejo más su conjugado, y queda:
(z + zc)2 = (1/3 + 4*i + 1/3 - 4*i)2 = (2/3)2 = 4/9 (1).
Luego, planteas la expresión del triple del número complejo, y queda:
3*z = 3*(1/3 + 4*i) = 1 + 12*i (2).
Luego, tienes la expresión compleja de tu enunciado:
(z + zc)2/(3*z) = sustituyes las expresiones señaladas (1) (2), y queda:
= (4/9)/(1 + 12*i) = multiplicas al numerador y al denominador por (1 - 12*i), y queda:
= (4/9)*(1 - 12*i) / (1 + 12*I)*(1 - 12*i) = distribuyes en el denominador, reduces términos semejantes, resuelves, y queda:
= (4/9)*(1 - 12*i) / 145 = resuelves la división entre números racionales, y queda:
= (4/1305)*(1 - 12*i) = distribuyes, y queda:
= 4/1305 - (16/435)*i.
Espero haberte ayudado.
-
Uriel Dominguez
el 5/2/19 -
Amin zine
el 5/2/19 -
Usuario eliminado
el 5/2/19
¿Esto está bien?, es que no estoy seguro, ya que he visto otras soluciones que en la matriz final hay menos unos. Gracias de antemano :).
David
el 21/2/19Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Daniel202
el 5/2/19
