Foro de preguntas y respuestas de Matemáticas

Los foros de unicoos se han unificado en nuestra nueva plataforma beUnicoos. Para dejar nuevas preguntas deberás hacerlo allí, donde además podrás encontrar nuevas asignaturas y herramientas para ayudarte más con tus estudios.

Ir a beUnicoos

Ikram Ammari
el 17/1/19

Tengo un problema de matemáticas que dice "En una pastelería han preparado los primeros polvorines artesanos de la temporada. Han intentado agruparlos en bandejas de 12,15,20 unidades, pero en todos los casos le sobran 7 polvorones han preparado?
-escribe 3 respuesta posibles, ya que no tienes suficiente información para estar seguro de cual es la respuesta"
Y tengo que usar el MCD Y MCM
Por favor como lo resolvería? Gracias

••1 voto/s
•
Antonio
el 17/1/19
como el mcm(12,15,20)=60
será entonces
60·1+7=67 polvorines
60·2+7=127 polvorines
60·3+7=187 polvorines

•2 voto/s
•

Cancelar
Usuario eliminado
el 17/1/19

hola buen día, tengo una duda con este ejercicio no se como resolverlo, podrías por favor ayudarme, seria de gran ayuda

••0 voto/s
•
Antonius Benedictus
el 17/1/19

•1 voto/s
•

Cancelar
Miriam Gonzalez
el 17/1/19

Hola. Lo intente volver a hacer pero no entiendo lo que hay que hacer a partir de ahí

••0 voto/s
•
Antonius Benedictus
el 17/1/19
No se ve nada.

•1 voto/s
•
Miriam Gonzalez
el 17/1/19
perdón.

•0 voto/s
•
Guillem De La Calle Vicente
el 17/1/19
Buenas Miriam,
Recuerda que un producto de dos factores es positivo si y sólo si los dos factores tienen el mismo signo. Por lo tanto, para que x*(raíz(3)/4 x -3) sea positivo, tenemos dos casos:
1) x > 0 y que raíz(3)/4 x -3 > 0
2) x < 0 y que raíz(3)/4 x -3 < 0.
Tenemos que resolver los dos sistemas de inecuaciones con una incógnita y vemos que la única solución positiva es la que te he dado porque x tiene que ser positivo (es una longitud).

Saludos.

•1 voto/s
•

Cancelar
Rubén
el 17/1/19

Hola unicoos, me pueden ayudar con este ejercicio?: demuestra por inducción que n! >3^(n-2) para todo n mayor o igual que 3.

••0 voto/s
•
Antonius Benedictus
el 17/1/19

•1 voto/s
•

Cancelar
Miriam Gonzalez
el 17/1/19

Hola. ¿Como haríais este problema con inecuaciones?

••0 voto/s
•
Guillem De La Calle Vicente
el 17/1/19

•3 voto/s
•
Miriam Gonzalez
el 17/1/19
muchas gracias!!!

•0 voto/s
•

Cancelar
Miriam Gonzalez
el 17/1/19

Hola. ¿Me podríais explicar como se hacen estas fracciones?
15/14-15/21

••0 voto/s
•
César
el 17/1/19
Suma de fracciones con mínimo común múltiplo

Suma de fracciones con mínimo común múltiplo

•1 voto/s
•
Miriam Gonzalez
el 17/1/19
Gracias

•0 voto/s
•
Guillem De La Calle Vicente
el 17/1/19

•3 voto/s
•

Cancelar
Marina
el 17/1/19

Hola, tengo una duda de un ejercicio de física de cinemática, pero en este caso mi fallo está al despejar si pueden ayudarme a terminarlo, no se cómo acabarlo. Mil gracias.

••0 voto/s
•
César
el 17/1/19
que variable quieres despejar?

•0 voto/s
•
Marina
el 17/1/19
Perdona se me había olvidado comentarlo, la velocidad en función del ángulo

•0 voto/s
•
Guillem De La Calle Vicente
el 17/1/19

•1 voto/s
•
Marina
el 17/1/19
Muchas gracias Guillem.
Y si quisiese despejar el ángulo, al tener tangente y coseno, ¿se podría?

•0 voto/s
•
Guillem De La Calle Vicente
el 17/1/19

•0 voto/s
•

Cancelar
Marcos Gallego Villalba
el 17/1/19

Buenas tardes, ¿habría posibilidad de ver algún vídeo de como resolver problemas de sistemas de ecuaciones?

••0 voto/s
•
Guillem De La Calle Vicente
el 17/1/19
Buenas Marcos. Te paso los vídeos de sistemas de ecuaciones:
https://www.unicoos.com/video/matematicas/2-eso/ecuaciones/sistemas-de-ecuaciones/sistema-de-ecuaciones-metodo-de-igualacion
https://www.unicoos.com/video/matematicas/4-eso/ecuaciones-y-sistemas/sistemas-no-lineales-de-ecuaciones/sistema-de-ecuaciones-no-lineal
https://www.unicoos.com/video/matematicas/1-bachiller/ecuaciones-y-sistemas/sistemas-de-ecuaciones/sistema-de-ecuaciones-con-4-incognitas-reduccion-gauss
https://www.unicoos.com/video/matematicas/2-bachiller/sistemas-de-ecuaciones/metodo-de-gauss/discutir-un-sistema-metodo-de-gauss
https://www.unicoos.com/video/matematicas/2-bachiller/sistemas-de-ecuaciones/teorema-de-rouche/discutir-un-sistema-01-rouche
https://www.unicoos.com/video/matematicas/2-bachiller/sistemas-de-ecuaciones/regla-de-cramer/sistema-de-ecuaciones-metodo-de-cramer
https://www.unicoos.com/video/matematicas/2-bachiller/sistemas-de-ecuaciones/resolucion-de-sistemas/sistema-compatible-indeterminado-01
Si eres catalán, te invito a visitar mi canal donde también encontraras videos de "sistemas de ecuaciones": https://www.youtube.com/channel/UCtlms7lPehkqvVyk2CBdwQA
Saludos!

•2 voto/s
•

Cancelar
dovigame
el 17/1/19

Hola unicoos me resulta difícil resolver estos dos ejercicios, lo he intentado pero no me sale bien

••0 voto/s
•
César
el 17/1/19
1

•0 voto/s
•
Guillem De La Calle Vicente
el 17/1/19

•1 voto/s
•
Guillem De La Calle Vicente
el 17/1/19

•1 voto/s
•
Guillem De La Calle Vicente
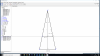
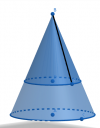
el 17/1/19
César, en la aplicación fíjate que el radio del cono grande es 15 cm, y no 15/2. Luego, x = r = 10 cm y ya nos cuadran todos los resultados! Lo he dibujado con GeoGebra 3D y el radio del cono pequeño tiene que ser 10 cm, porque si es de 5 cm, el cono pequeño es interior al grande!

Saludos crack!

•0 voto/s
•
Guillem De La Calle Vicente
el 17/1/19
dovigame, el segundo ejercicio es igual al primero cambiando los datos del enunciado! Lo puedes intentar y nos cuentas!

Te paso los resultados que me han salido:
- Radio mayor del tronco de cono: 12 cm
- Radio menor del tronco de cono: 9 cm
- Altura del tronco de cono: 4 cm
- Generatriz del tronco de cono: 5 cm
- Área lateral: 329,7 cm²
-Área total: 781,86 cm²
- Volumen: 1394,87 cm³

Saludos.

•0 voto/s
•
César
el 17/1/19
Gracias Guillem , has sido astuto observador jeje

•0 voto/s
•
dovigame
el 10/9/21
Necesito información sobre algun TFG que tenga como tamiz de enfoque "Resolución de problemas con sistemas de ecuaciones con dos incógnitas. Este ha sido mi tema de trabajo fin de grado y quiero comenzar a redactarlo , se que me he ausentado mucho y , eso ha sido por las clases y e l tiempo

•0 voto/s
•

Cancelar
marta Sanz
el 17/1/19

Sea p un polinomio monico de grado impar. Demuestra que p tiene al menos una raíz. Demuestre que existe Demuestra que existe a < 0 tal que p(a) < 0 y b > 0 tal que p(b) > 0. truco:
considera los limites de x infinito and x -infinito de p(x).

otro apartado
Sea p un polinomio mónico de grado n y sea r una raíz de p.
Sea q el polinomio de grado n-1 tal que p (x) = (x-r) q (x)
demuestra que q es monic.(ya )
Demuestre que los coeficientes de p y q cumplen que pi + 1 = q i – r qi + 1 para i = 0, ... .n-2 y explica cómo usar esto de manera iterativa para calcular los coeficientes numéricamente dados r y los coeficientes de p. (me falta)
No se si esta explicacion es valida
La iteración en computación es la técnica que marca un bloque de declaraciones dentro de un programa de computadora para un número definido de repeticiones.
Hay que hacerlo para i=0, i=1….i=j+1
p1=q0-rq1lo metes en el polinomio p (x) = (x-r) q(x)
p2=q1-rq2
…..
pi+1=qi-rqi+1p

y otro apartado es

••0 voto/s
•
Antonius Benedictus
el 17/1/19
¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

•0 voto/s
•

Cancelar