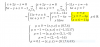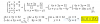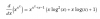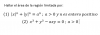-
Pau Martin
el 15/11/18Estoy estancado en este problema sobre Rectas tangentes.
En que punto de la curva de la función f(x)= x·lnx-x el pendiente de la recta tangente vale 1? Alguien me lo puede resolver o explicarme como se resuelve por favor?
Antonio
el 15/11/18 -
Ali Hussain
el 15/11/18Greetings everyone
Need solution with some explanation for this question
Guillem De La Calle Vicente
el 15/11/18(i) In the histogram, 16 poiling stations are represented. Total number: 16 + 8 + 12 + 10 = 46
(ii) [15, 18) --> 16 poiling stations per hour
[18, 23) --> 8 poiling stations per hour
[23, 25) --> 12 poiling stations per hour
[25, 31] --> 10 poiling stations per hour
(iii) Class mark for each interval: (18+15)/2=16.5 ; (23+18)/2 = 20.5 ; (23+25) / 2 = 24; (25+31) / 2 = 28
Mean = (16.5*16 + 20.5*8 + 24*12 + 28*10) / 46 = 21.65
(iv) 7:00 a.m - 11:00 p.m ---> 16 hours
21.65 * 11 = 238.15
-
MDY01
el 15/11/18 -
Pau Martin
el 15/11/18Hola buenas, sobre la recta tangente... Cuando una pendiente es perpendicular a otra decimos que m·m(perpendicular)= -1, pero cuando es paralela, cual es la formula?
-
Lau
el 15/11/18 -
Matias
el 15/11/18
Hola unicoos. Me ayudan con el punto d?? No importa como saque la serie y los resultados, solo quisiera que me den una mano con el ultimo punto.
Creo que en x=0 converge a 1 pero en x=1 no esta definida
Antonius Benedictus
el 15/11/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Armando Socastro
el 15/11/18Buenas tardes,
tengo una duda con un problema de combinatoria.
"Cuantas palabras distintas se pueden formar con las letras de la palabra PERSONA si P aparece antes de R y N aparece antes de R"
Como se calcula?
Yo lo pense de la siguiente manera Coloco 4 letras (4!) y solo me queda una manera de colocar PNR
Gracias.
Antonio Silvio Palmitano
el 15/11/18Observa que tienes siete elementos distintos, y que dos de ellos (N y P) deben ubicarse antes del elemento R,
por lo que tienes que elemento R puede ocupar desde el tercer lugar hasta el séptimo lugar, por lo que tienes distintas opciones:
1)
El elemento R ocupa el tercer lugar:
- - R - - - -,
ubicas los elementos N y P en dos de los lugares "delanteros" y tienes:
P(2,2) = 2!/0! = 2 opciones;
luego ubicas las cuatro letras restantes en los demás lugares, y queda:
P(4,4) = 4!/0! = 24 opciones;
luego, por el principio de multiplicación tienes:
N1 = 2*24 = 48 opciones.
2)
El elemento R ocupa el cuarto lugar:
- - - R - - -,
ubicas los elementos N y P en dos de los lugares "delanteros" y tienes:
P(3,2) = 3!/1! = 6 opciones;
luego ubicas las cuatro letras restantes en los demás lugares, y queda:
P(4,4) = 4!/0! = 24 opciones;
luego, por el principio de multiplicación tienes:
N2 = 6*24 = 144 opciones.
3)
El elemento R ocupa el quinto lugar:
- - - - R - -,
ubicas los elementos N y P en dos de los lugares "delanteros" y tienes:
P(4,2) = 4!/2! = 12 opciones;
luego ubicas las cuatro letras restantes en los demás lugares, y queda:
P(4,4) = 4!/0! = 24 opciones;
luego, por el principio de multiplicación tienes:
N3 = 12*24 = 288 opciones.
4)
El elemento R ocupa el sexto lugar:
- - - - - R -,
ubicas los elementos N y P en dos de los lugares "delanteros" y tienes:
P(5,2) = 5!/3! = 20 opciones;
luego ubicas las cuatro letras restantes en los demás lugares, y queda:
P(4,4) = 4!/0! = 24 opciones;
luego, por el principio de multiplicación tienes:
N4 = 20*24 = 480 opciones.
5)
El elemento R ocupa el séptimo lugar:
- - - - - - R,
ubicas los elementos N y P en dos de los lugares "delanteros" y tienes:
P(6,2) = 6!/2! = 360 opciones;
luego ubicas las cuatro letras restantes en los demás lugares, y queda:
P(4,4) = 4!/0! = 24 opciones;
luego, por el principio de multiplicación tienes:
N5 = 360*24 = 8640 opciones.
Luego, por el principio de adición, tienes la cantidad de palabras que se pueden formar con la letra N y la letra P ubicadas antes de la letra R:
N = 48 + 144 + 288 + 480 + 8640 = 9600.
Espero haberte ayudado.
Armando Socastro
el 16/11/18 -
Alejandro
el 15/11/18Hola, me pueden ayudar con esta derivada por definición de limites.
Deantemano gracias.
-
Giampier Alfonso Carrion Huaripata
el 15/11/18Buenas me pueden ayudar con estos ejercicios:
Antonius Benedictus
el 15/11/18¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David Calle ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Lautaro
el 15/11/18
