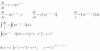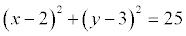-
Bryan
el 22/9/18 -
ivana
el 21/9/18Tengo que encontrar las cotas de esta sucesión an=(1-5/n)2n y no se cómo encontrar la cota inferior ya que empieza siendo una sucesión decreciente y en algún n0 empieza a ser creciente acercándose en el infinito a e10 . Debo encontrar ese n0 y no se cómo. Una ayudita por favor
Diaz Daniel Victor
el 22/9/18Podés resolver casi cualquier ejercicio matemático con esa app, tal vez no sea lo mejor pero muchas veces nos confundimos en un pequeño detalle o no sabemos por donde comenzar y esto nos puede ayudar... no recomiendo usarlo siempre porque crea una dependencia pero podemos comprobar algunos ejercicios, yo no lo uso porque es para Android y tengo otro SO pero lo usé hace un tiempo y me funcionaba de maravilla. No sé cuánto tiempo funcione el link
http://www.mediafire.com/file/0djj1ghxlofandf/Wolfram_Alpha.apk/file
-
Julián Orozco
el 21/9/18Hola, no puedo con este problema ayuda!!
Encuentra la ecuación general de la circunferencia de Radio 5 y que pasa por el punto (2,3)
-
Julián Orozco
el 21/9/18Hola.
Alguien me puede ayudar con este problema.
Una recta pasa por los puntos A(-2,3) y B(-2,-1) encuentra la distancia entre los puntos y su ecuación simétrica.
-
Desconocido
el 21/9/18Está está propiedad bien demostrada mediante inducción matemática?
n! ≤ n^n, ∀n ≥ 1
Probando con n = 1,
1! = 11^1 = 1
Con lo que se cumple que 1 <= 1Asumimos que se cumple para (n-1)! ≤ (n-1)^(n-1), ∀n > 1
Ahora toca demostrar que n! ≤ n^n
n! ≤ n^n ⇔ (n-1)! * n ≤ n*n^(n-1) ⇔ (n-1)! ≤ n^(n-1) ⇔ n^(n-1) ≤ n^n, ∀n > 1
Quedaría demostrado? Gracias.
Diaz Daniel Victor
el 22/9/18Me parece que está bastante bien el planteamiento podría ser recomendable demostrar para el siguiente de n porque la propiedad dice que se cumple para n! ≤ n^n, ∀n ≥ 1
por lo tanto la hipótesis sería:
se cumple para n! ≤ n^n, ∀n ≥ 1
la demostración sería intentar ver si se cumple para el siguiente
(n+1)! ≤ n^(n+1) ⇔ n!*n ≤ n^n *n ⇔ n! ≤ n^n, ∀n ≥ 1
Así llegás a lo que dice la propiedad!
-
Juan C
el 21/9/18 -
Albert Loðbrók
el 21/9/18 -
Mariano Cornejo
el 21/9/18 -
Mariano Cornejo
el 21/9/18Hola unicoos quería saber cómo hago el ejercicio 8,
eso es todo gracias.
Antonio Silvio Palmitano
el 21/9/18Puedes plantear la expresión factorizada del polinomio:
P(x) = A*(x-a)*(x-b)*(x-c),
donde A es el coeficiente principal, y donde a, b y c son sus raíces.
Luego, tienes en tu enunciado:
A = 2, a = 2, b = -3, c = 7;
luego, reemplazas valores en la expresión del polinomio, y queda:
P(x) = 2*(x-2)*(x+3)*(x-7).
Espero haberte ayudado.
-
carmela
el 21/9/18Hola. No soy capaz de resolver esta ecuacion matricial
Antonio Silvio Palmitano
el 21/9/18Efectúas la multiplicación de matrices en el primer miembro (observa que queda una matriz de tres filas y una columna), y la ecuación matricial de tu enunciado queda:
0x - 1y + 1z 0
0x - 3y + 3z = 0
0x + 0y - 2z 0,
luego, como tienes una igualdad entre matrices, igualas elemento a elemento (observa que cacelamos los términos nulos, y queda el sistema de tres ecuaciones con tres incógnitas:
-y + z = 0,
-3y + 3z = 0,
-2z = 0, aquí divides por -2 en ambos miembros, y queda: z = 0;
luego, reemplazas el valor remarcado en las dos primeras ecuaciones (observa que cancelamos los términos nulos), y queda:
-y = 0, aquí divides por -1 en ambos miembros, y queda: y = 0;
-3y = 0;
luego, reemplazas el último valor remarcado en la última ecuación, resuelves el primer miembro, y queda:
0 = 0, que es una Identidad Verdadera,
por lo que puedes concluir que el sistema es compatible determinado y tiene infinitas soluciones y, por lo tanto la ecuación matricial también tiene infinitas soluciones, porque la incógnita x puede tomar cualquier valor real, la incógnita y es igual a cero y la incógnita z es igual a cero;
luego, la matriz solución de la ecuación matricial queda:
X =
x
0
0,
con x ∈ R.
Espero haberte ayudado.
