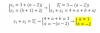-
Hola! Probabilidad condicional, ejercicio de parcial.
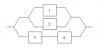
Considere el sistema de componentes conectados como en la figura siguiente.
Los componentes 1 y 2 están conectados en paralelo, de modo que el subsistema
funciona si y sólo si funciona el componente 1 o el componente 2; como los
componentes 3 y 4 están conectados en serie, ese subsistema funciona si y sólo
si 3 y 4 funcionan. Si los componentes funcionan de manera independiente uno
de otro y para cada componente la probabilidad de que funcione es 0.9, calcule
la probabilidad de que el sistema funcione. Calcular la probabilidad de que el componente 1 no funcione si se sabe que el sistema sí funciona.
Muchas gracias!
Considere el sistema de componentes conectados como en la figura siguiente. Los componentes 1 y 2están conectados en paralelo, de modo que el subsistema funciona si y solo si funciona 1 o 2; como 3 y4 están conectados en serie, ese subsistema funciona
están conectados en paralelo, de modo que el subsistema funciona si y solo si funciona 1 o 2; como 3 y4 están conectados en serie, ese subsistema funciona
-
Hola unicoos.
Calculo vectorial.
a) r(t)= 8t î - 1/t j
b) r(t)= ln(5t+1)î - 1/raiz(t^2 -9) j + cos(t) k
Para que valores de t la funcion vectorial es continua.
Ayuda por favor y de antemano gracias.
Antonio Silvio Palmitano
el 19/9/18Observa que para que una función vectorial sea continua en un intervalo D se tiene que cumplir que todas sus componentes también sean continuas en dicho intervalo.
a)
Tienes que las componentes:
x(t) = 8t, que es continua en (-∞,+∞),
y(t) = -1/t, que es continua en (-∞,0) ∪ (0,+∞);
por lo tanto, tienes que la función vectorial es continua en el intervalo que es intersección de los tres intervalos: D = (-∞,0) ∪ (0,+∞).
b)
Tienes que las componentes:
x(t) = ln(5t+1), que es continua en (-1/5,+∞),
y(t) = 1/√(t2-9), que es continua en (-∞,-3) ∪ (3,+∞),
z(t) = cos(t), que es continua en (-∞,+∞);
por lo tanto, tienes que la función vectorial es continua en el intervalo que es intersección de los tres intervalos: D = (3,+∞).
Espero haberte ayudado.
-
Neofito 007
el 19/9/18Propiedades :
* Cos2(u) - Sen2(u) = Cos(2u)
* 2Sen(u) Cos(u) = Sen(2u)
Parte izquierda :
Cos2(x/2) - Sen2(x/2) = Cos( 2(x/2) ) = Cos(x) , también
2Sen(x/2) Cos(x/2) = Sen( 2(x/2) ) = Sen(x) , entonces queda
I = Cosx + Senx
Elevando ambos lados al cuadrado queda
(Cosx + Senx)2 = 1 + Sen(2x)
Cos2x + Sen2x + 2Senx Cosx = 1 + Sen(2x)
1 + Sen(2x) = 1 + Sen(2x) , .......Recordar la identidad Sen2x + Cos2x = 1
Como cumple la igualdad es una identidad . -
Hola buenas tardes, tengo una duda con respecto a este límite, sinceramente no siento que lo haya realizado bien. Me podrían decir en que me equivoqué?

Diaz Daniel Victor
el 19/9/18Cuando haces el cambio de variable no estás haciendo mucho solo le lamas u a x (solo para aclarar)... Deberías probar primero que clase de límite es reemplazando el valor al que tiende x... osea al Lím (x→0) de [cos (3.x) -1] / (2. x^2) = [cos (3.0) -1] / (2. 0^2)... cos 0 =1... y esto da (1-1)/0 = 0/0 osea el primer caso deberías aplicar
Neofito 007
el 19/9/18Es un límite del tipo 0/0 , es indeterminado se tiene que levantar la indeterminación .
Allí estás aplicando las propiedades de multiplicación de límites pero ocurre que al hacer ello te encuentras con
otra forma indeterminada que es (infinito)*(cero) , esto último no es levantar la indeterminación porque de una forma indeterminada pasas a otra también indeterminada .
Una forma para este caso es aplicar la regla de L Hopital que es derivar a numerador y denominador , hasta levantar la indeterminación.
Otra manera sin derivar , hay que llevarlo a límites conocidos .
Por propiedad trigonométrica 1 - Cos(2k) = 2Sen2 k , aplicando esto al numerador se tiene
Cos(3x) - 1 = - [ 1 - Cos(3x) ] = - 2Sen2(3x/2)
el denominador se puede poner como 2 *(4/9) * (3x/2)2 , la idea es darle forma
Reemplazando queda :
L = Limit x-->0 [- 2Sen2(3x/2) ] / [ 2 * (4/9) * (3x/2)2 ] = - (9/4) Limit x-->0 [ Sen(3x/2) / (3x/2)]2Acá ya se tiene un límite conocido Limit u-->0 Senu / u = 1
L = - (9/4)(1)2 = - 9/4
-
Ejercicio 2 punto b, función f(x)...la función sería continua en x=1? Dado que f(1) = 2....y si se realiza el límite también se obtiene 2

Diaz Daniel Victor
el 19/9/18El lím que se obtiene es -∞ por lo tanto como no coinciden los límites es discontinua... si probas por derecha acercandote en milésimos a 1 vas a ver que va ir creciendo el resultado positivamente y si lo probas por derecha crece negativamente.... reemplazá valores como (0,8899; 0,9; 0,99; 0,999 y 1,01; 1,009; 1,00001) así se prueban los límites laterales.
Diaz Daniel Victor
el 19/9/18Neofito 007
el 19/9/18Quizá haya una confusión, el límite no es lo mismo que la función evaluada en un punto , justamente esto es lo que se tiene que averiguar mediante las operaciones para poder saber si en un punto dado es continua o no lo es .
Hay que tener en cuenta que " al límite no le interesa como es la función en ese punto " puede que exista , puede que sean diferentes , iguales o lo que sea .
Continuidad en x = 1
a) x = 1 pertenece al dominio ? ... Sí
b) Calcular límite cuando x-->1 , hay que analizar los límites laterales :
* Cuando tiende a 1 por la derecha x > 1 ==> x - 1 > 0 .....el numerador tiende a ( - 2 ) , el denominador tiende a cero pero es positivo , entonces el límite es ( - infinito ) .... algo así : -2 / 0+ = - infinito , ya que (-) / (+) = (-)
** Cuando tiende a 1 por la izquierda x < 1 ==> x - 1 < 0 .....el numerador tiende a ( - 2 ) , el denominador tiende a cero pero es negativo , entonces el límite es ( + infinito ) ... algo así : -2 / 0- = + infinito , ya que (-) / (-) = (+)
Conclusión el límite no existe .
c) El límite debe ser igual a la función en x=1 , esto ya ni lo vemos porque el paso (b) dice que el límite no existe .
Para la continuidad se deben cumplir esas 3 cosas i) 1 debe pertenecer al dominio , ii) Debe existir el límite cuando x-->1 , iii) limit x-->1 f(x) = f(1) .
Entonces como la segunda condición no se cumple y por ende tampoco la tercera entonces la función no es continua en x = 1
Además la parte (b) indica que allí existe una discontinuidad esencial o no evitable , específicamente discontinuidad asintótica .
Facu Imfeld
el 19/9/18Neofito supongo que estás analizando la función cuando x distinto de 1, la pregunta es, ¿porque? es decir, si tengo que la función vale 2 cuando x = 1 y vale lo otro para x distinto de 1, porque analizaría el límite en la otra función y no en 2, donde si está definido para x = 1 que es donde me piden calcular el límite, no sé si fui claro
Neofito 007
el 19/9/18Hola Facu , justamente por lo indicado arriba : para el límite no se analiza ni se tiene en cuenta cómo es la función en ese punto , sino lo que importa es cómo se comporta la función cuando x se aproxima a 1 (no su valor cuando x=1 osea f(1) ), entonces se analiza la función cuando x se acerca a 1 por la derecha y por la izquierda . Esto lo puedes verificar en la definición de límite cuando dice 0 < |x - x0| < δ fíjate acá que x ≠ x0
Por eso la frase de arriba que " al límite no le interesa como es la función en ese punto "
Lo anterior es muy importante que quede claro . Ahora responderé porqué analizar el límite allí :
Lo que se debe analizar es cuando x se acerca a 1 , es decir cuando x no es 1 pero está muy cerca a 1 , en otras palabras cuando es diferente de 1 y cuando x ≠ 1 me dan una regla de correspondencia (2x^2 + x - 5) / (x-1) esta se usa para calcular el límite ya que con esta regla de correspondencia voy a poder conocer el comportamiento de la función cuando x >1 y cuando x < 1 ( x muy cercano a 1) que es el propósito del límite.
Entonces hay que quitarse la idea que límite es lo mismo que evaluar la función en un punto , esto obviamente se consigue comprendiendo y estudiando un poco más los conceptos .
Otro asunto , lo que piden no es si está definida o no en x=1 (obviamente sí lo está) sino lo que piden es analizar la continuidad en x=1 y para ello se deben cumplir 3 condiciones necesarias y suficientes que arriba indico .