-
Gena Shcherbakov
el 8/5/18
estoy haciendo ejercicios sobre ajuste de ecuaciones químicas y me sale
a=c
3c=2d
2b=d
se que debo coger un número para ponerle a la c y necesito ayuda pls
Antonio Silvio Palmitano
el 9/5/18Observa que tienes tres ecuaciones con cuatro incógnitas.
En la primera ecuación tienes: a = c (1).
En la segunda ecuación divides por 2 en ambos miembros, y tienes: (3/2)c = d (2).
Luego, sustituyes la expresión señalada (2) en la tercera ecuación, y queda:
2b = (3/2)c, luego divides por 2 en ambos miembros, y queda: b = (3/4)c (3).
Luego, observa las ecuaciones señaladas (1) (2) (3) y tienes que has despejado tres de las incógnitas (a, b y c), y sus expresiones son funciones de la incógnita c:
a = c,
b = (3/4)c,
d = (3/2)c.
Luego, observa que para que todas las incógnitas correspondan a números naturales, tienes que la incógnita c debe ser un múltiplo de 4, por lo que tienes:
1)
Con c = 4:
a = 4,
b = (3/4)(4) = 3,
d = (3/2)(4) = 6;
2)
Con c = 8:
a = 8,
b = (3/4)(8) = 6,
d = (3/2)(8) = 12;
y así puedes continuar con los demás casos, y tomar el que corresponda a tu problema.
Espero haberte ayudado.
-
Andrea
el 8/5/18
Alguien que me pueda ayudar con el apartado d?? Como calculo el desplazamiento? Y la velocidad utilizo 5 como vf y 2 como v inicial? Como se calcula la media aritmetica de la velocidad?
-
Andrea
el 8/5/18Un paracaidista salta desde una altura de 3km.Tras caer libremente durante 50m, abre su paracaídas y desde ese momento cae con velocidad constante.
a)Cuánto ha durado la caída libre? B)Cúal es su velocidad cuando abre el paracaídas
El apartado a me da 3,2 s pero no sé como hacer el apartado b, ayuda !!
-
Usuario eliminado
el 8/5/18Tenemos una bobina formada por 100 espiras y tiene una longitud de 50 cm i cuando se cierra el circuito al cual esta conectada, pasa una corriente de 15 A.
a) Encuentra el campo magnético que crea esta bobina.
b) Cuál será el sentido del corriente eléctrico de la bobina, cuál será el sentido del campo magnético que crea.
-
Augusto Mn
el 8/5/18hola necesito ayuda con esto. gracias
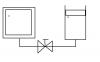
Problema 12: Se tiene un sistema cerrado
compuesto por dos cilindros como se indica en
la figura en el recipiente A, totalmente
adiabático, se tienen 10 Kg de aire a 10 atm y
500K, mientras que en el recipiente, que no es
adiabático; B se tiene 10 Kg de aire a 5 atm y
300 K. Se abre la válvula y se espera lo
suficiente hasta que se logre el equilibrio
termodinámico. Una vez que el equilibrio se ha logrado, calcular:
a) Volumen final; b) Trabajo y calor intercambiado con el medio.
DATOS:
Cv aire = 0,17 Kcal/Kg. K – Cp aire = 0,24 Kcal/Kg. K – 1 Kcal = 427 Kgm.
La temperatura del ambiente es 300 K y la Presión 1 atm
-
Winie Mesa
el 8/5/18Una partícula A choca elásticamente con otra partícula de masa B que inicialmente está en reposo. La partícula A que impacta tiene una rapidez inicial de 4,90 m/s y hace una colisión oblicua con la partícula B, como muestra la Figura. Después de la colisión, la partícula A se aleja en un ángulo de θ =24,4° hacia la dirección de movimiento original y la partícula B se desvía a un ángulo ɸ con el mismo eje. Encuentre las magnitudes de velocidad finales de las dos partículas y el ángulo ɸ.
Nota: Asuma que las partículas tienen igual masa.
Porfa necesito ayuda
Antonio Silvio Palmitano
el 8/5/18Vamos con una orientación para abordar el problema.
Plantea un sistema de referencia con eje OX con dirección y sentido acorde al desplazamiento de la partícula A antes del choque, y con eje OY perpendicular al anterior, con sentido positivo acorde a la componente paralela del desplazamiento de la partícula A después del choque.
Luego, tienes que se conserva el impulso (o cantidad de movimiento) y, como el choque es elástico, tienes que también se conserva la energía mecánica (en este caso solo cinética de traslación), por lo que puedes plantear tres ecuaciones: una con las componentes de la cantidad de movimiento en la dirección del eje OX, otra con las componentes de la cantidad de movimiento en la dirección del eje OY, y otra con las expresiones de la energía cinética, y queda (indicamos con M a la masa de cada partícula):
M*4,90 + M*0 = M*vA*cos(24,4°) + M*vB*cosΦ,
M*0 + M*0 = M*vA*sen(24,4°) + M*vB*senΦ,
(1/2)*M*4,902 + (1/2)*M*02 = (1/2)*M*vA2 + (1/2)*M*vB2.
Cancelas términos nulos, divides por M en todas las ecuaciones, multiplicamos por 2 en todos los términos de la tercera ecuación, y queda:
4,90 = vA*cos(24,4°) + vB*cosΦ,
0 = vA*sen(24,4°) + vB*senΦ,
4,902 = vA2 + vB2.
Luego, tienes un sistema de tres ecuaciones con tres incógnitas. Haz el intento de resolverlo, y si te resulta necesario, no dudes en volver a consultar.
Espero haberte ayudado.
-
Edingsong Fabiam Toloza
el 8/5/18Buenas noches, por favor quien me puede ayudar en este ejercicio.
Por una tubería horizontal, circula agua de mar, como parte de un proyecto de investigación, desarrollado por uno de los grupos de física de la UNAD. La tubería inicialmente tiene un diámetro de 540 cm y se estrecha hasta tener un diámetro de 3,92 cm . Uno de los objetivos del proyecto, consiste en determinar el caudal volumétrico del agua de mar. Cuando el agua de mar fluye por la tubería, la presión manométrica en las dos secciones son de 30.4x10^3 kPa y 25.2x10^3 kPa respectivamente. Con base en esta información, determine el valor del caudal volumétrico o gasto del agua de mar.
Raúl RC
el 8/5/18Lo siento, pero no atendemos dudas universitarias que no sean sobre los videos que el profe grabó especificamente...como por ejemplo éste...pero poco mas puedo ayudarte, espero lo entiendas.
-
Jampier
el 8/5/18que debo estudiar primero en fisica , ecuaciones dimensionales?? , gracias
Guillem De La Calle Vicente
el 8/5/18 -
Tyssa Martin Fernandez
el 8/5/18La sección ancha de un tubo de Venturi horizontal tiene un diámetro de 4 cm, y la sección estrecha tiene un diámetro de 2 cm. Al circular agua, la diferencia de presiones entre ambas secciones es de 3000 Pa. a) Calcular la velocidad del agua en ambas tuberías. Sol: 0,63 y 2,53 m/s b) Determinar el caudal del flujo.
Solo quería saber como se calcula el caudal del flujo, gracias.
-
Tyssa Martin Fernandez
el 7/5/18En condiciones estándar, la densidad del aire es de 1,29 kg/m3 y la del helio es de 0,178 kg/m3 . Si queremos levantar una masa de 200 kg con un globo lleno de helio, ¿qué volumen debe tener?
Antonio Silvio Palmitano
el 8/5/18Observa que sobre el globo actúan tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos:
Peso del globo: Pgl = δHe*Vgl*g, vertical, hacia abajo;
Empuje del aire sobre el globo: E = δai*Vgl*g, vertical, hacia arriba;
Peso de la masa: PM = M*g, vertical, hacia abajo.
Luego, observa que si el globo asciende con velocidad constante, tienes que se encuentra en equilibrio, por lo que planteas la Primera Ley de Newton, y queda:
E - Pgl - PM = 0, sumas PM en ambos miembros, y queda:
E - Pgl = PM, sustituyes expresiones, y queda:
δai*Vgl*g - δHe*Vgl*g = M*g, divides por g en todos los términos de la ecuación, y queda:
δai*Vgl - δHe*Vgl = M, extraes factor común en el primer miembro, y queda:
(δai - δHe)*Vgl = M, divides por (δai - δgl) en ambos miembros, y queda:
Vgl = M/(δai - δHe),
y solo queda que reemplaces valores y hagas el cálculo.
Espero haberte ayudado.
