-
Un objeto de masa 1 kg se lanza hacia arriba desde la superficie de
la Tierra con velocidad inicial de 3 m/s. Sabiendo que la fuerza de
rozamiento con el aire es de v^2/10 newtons, donde v es la velocidad del
objeto, se pide
a. Obtener el tiempo que el objeto tarda en pararse.No se como sacar la ecuación que lo relaciona, me pueden ayudar?
Antonio Silvio Palmitano
el 29/10/17Considera un sistema de referencia con un eje de posiciones (alturas) OY vertical, con sentido positivo hacia arriba, y observa que el objeto se desplaza hacia arriba, y que consideramos que el módulo de la aceleración gravitatoria terrestre es: g = 9,8 m/s2.
Luego, observa que sobre el objeto actúan dos fuerzas (observa que su masa es M = 1 Kg):
Peso: P = M*g = 1*9,8 = 9,8 N, vertical, hacia abajo;
Rozamiento del aire: fr = v2/10, vertical hacia abajo;
luego, aplicas la Segunda Ley de Newton y tienes la ecuación:
-P - fr = M*a, sustituyes expresiones, expresas a la aceleración en función de la velocidad, y queda:
-9,8 - v2/10 = 1*dv/dt, multiplicas por 10 en todos os términos de la ecuación, extraes factor común en el primer miembro, y queda:
-(98 + v2) = 10*dv/dt, haces pasaje de factor y de divisor para separar variables, y queda:
-dt = 10*dv/(98 + v2), que es la ecuación diferencial que necesitas, con sus variables separadas, y observa que su condición inicial es: v(0) = 3 m/s.
Luego, solo queda que resuelvas la ecuación.
Espero haberte ayudado.
-
hola quisiera la solucion a este ejercicio OJO no me sirve que busquen la solucion por internet y me hagan un corta y pega, pues quiero explicaciones - Un bloque de 2 kg de masa, que descansa sobre una superficie horizontal, está unido a un extremo de un muelle de masa despreciable y constante elástica 4,5 N m-1. El otro extremo del muelle se encuentra unido a una pared. Se comprime el muelle y el bloque comienza a oscilar sobre la superficie. Si en el instante t = 0 el bloque se encuentra en el punto de equilibrio y su energía cinética es de 0,90·10-3 J, calcule, despreciando los efectos del rozamiento: a) La ecuación del movimiento x(t) si, en t = 0, la velocidad del bloque es positiva. b) Los puntos de la trayectoria en los que la energía cinética del bloque es 0,30·10-3 J. el apartado a me da 0,02 y el b 0.011
Antonio Silvio Palmitano
el 29/10/17Establece un sistema de referencia con un eje de posiciones OX horizontal, con sentido positivo alejándose de la pared, y con origen en el punto de equilibrio.
Luego, puedes plantear la función posición:
x = A*sen(ω*t) (observa que se cumple la condición del enunciado: x(0) = 0),
luego tienes para la expresión de la función velocidad:
v = ω*A*cos(ω*t).
Luego, recuerda la relación entre coeficiente angular, constante elástica y masa del oscilador:
ω2 = k/M, reemplazas y queda: ω2 = 4,5/2 = 2,25, haces pasaje de potencia como raíz, y queda: ω = 1,5 rad/s;
luego reemplazas en las ecuaciones de posición y de velocidad, y quedan:
x = A*sen(1,5*t).
v = 1,5*A*cos(1,5*t).
Luego, plantea la expresión de la energía cinética en función del tiempo:
EC = (1/2)*M*v2, sustituyes, y queda:
EC(t) = (1/2)*2*1,52*A2*cos2(1,5*t), resuelves coeficientes, y queda:
EC(t) = 2,25*A2*cos2(1,5*t).
Luego, tienes el dato inicial:
EC(0) = 0,90*10-3 J,
sustituyes la expresión evaluada de la energía cinética en el primer miembro, y queda:
2,25*A2*cos2(1,5*0) = 0,90*10-3,
resuelves coeficientes en el primer miembro, y queda:
2,25*A2 = 0,90*10-3,
haces pasaje de factor como divisor, y queda:
A2 = 0,4,
haces pasaje de potencia como raíz, y queda:
A ≅ 0,6325 m, que es la amplitud de oscilación;
luego, reemplazas en las ecuaciones de posición y de velocidad, resuelves coeficientes, y quedan:
x ≅ 0,6325*sen(1,5*t), expresada en m,
v ≅ 0,9487*cos(1,5*t), expresada en m/s.
Luego, haces pasajes de factores como divisores, y las ecuaciones quedan:
x/0,6325 ≅ sen(1,5*t)
v/0,9487 ≅ cos(1,5*t),
elevas al cuadrado en ambos miembros, sumas miembro a miembro (observa que tienes identidad trigonométrica en el segundo miembro), y queda:
x2/0,4 + v2/0,9 = 1,
haces pasaje de término, y queda:
v2/0,9 = 1 - x2/0,4,
multiplicas por 0,9 en todos los términos de la ecuación, y queda:
v2 = 0,9 - 2,25*x2;
luego, planteas la expresión de la Energía Cinética, sustituyes y queda:
EC = (1/2)*M*v2 = (1/2)*2*(0,9 - 2,25*x2 = 0,9 - 2,25*x2;
luego, reemplazas el dato del enunciado (EC = 0,30*10-3 J), y queda:
0,30*10-3 = 0,9 - 2,25*x2,
haces pasajes de términos, y queda:
2,25*x2 = 0,8997,
haces pasaje de factor como divisor, y queda:
x2 ≅ 0,3999 ≅ 0,4,
haces pasaje de potencia como raíz, y tienes dos opciones:
x ≅ - 0,6325 m, y x ≅ 0,6325 m.
Espero haberte ayudado.
-
La posición de una partícula de masa M viene dada por las siguientes expresiones: 𝑋 = 𝐴 + 𝐵𝑡 − 𝐶𝑡 2 ; 𝑌 = 𝐷 + 𝐸𝑡 − 𝐹𝑐𝑜𝑠(𝐺𝑡); 𝑍 = 𝐻 + 𝐹𝑠𝑖𝑛(𝐺𝑡) Donde A, B, C, D, E, F, G y H son constantes.
a. Calcular las 3 componentes de la aceleración en función del tiempo.
En el a basicamente tengo que derivar dos veces para hallar las expresiones de la aceleracion o la pregunta trata sobre las componentes tangencial y normal de la aceleracion?
Antonio Silvio Palmitano
el 29/10/17Comienza por plantear las tres componentes de la velocidad, para ello derivas, y queda:
X ' = B - 2C*t,
Y ' = E + FG*sen(Gt),
Z ' = FG*cos(Gt),
luego, tienes la expresión vectorial de la velocidad:
v(t) = < X ' , Y ' , Z ' > = < B - 2C*t , E + FG*sen(Gt) , FG*cos(Gt) >.
Luego, planteas las tres componentes de la aceleración, para ello derivas nuevamente, y queda:
X ' ' = -2C,
Y ' ' = FG2*cos(Gt),
Z ' ' = -FG2*sen(Gt),
luego, tienes la expresión vectorial de la aceleración:
a(t) = < X ' ' , Y ' ' , Z ' ' > = < -2C , FG2*cos(Gt) , -FG2*sen(Gt) >.
Luego, puedes plantear para las componentes tangencial y normal de la aceleración
(observa que indicamos producto escalar con •,
y producto vectorial con x):
aT = ( v(t) • a(t) ) / |v(t)|,
aN = | v(t) x a(t) | / |v(t)|,
y solo queda que continúes la tarea.
Espero haberte ayudado.
Carlos
el 29/10/17Vale, es lo que tenia hecho hasta el momento, todo aclarado en el apartado a) pero luego en el apartado b) me preguntan : ¿Son la dirección y la magnitud de la aceleración independientes del tiempo?
Yo creo que se refieren a la tangencial(dirección) y la normal (magnitud) pero como se razona? la componente X no varia según el tiempo pero las otras 2 componentes sí por lo que aceleración normal solo es independiente en el componente X. Además, no se sabe que movimiento es no? porque si es rectilinio, la direccion es constante respecto del tiempo...
Antonio Silvio Palmitano
el 29/10/17Vamos con la magnitud de la aceleración:
|a(t)| = √( (-2C)2 + ( FG2*cos(G*t) )2 + ( -FG2*sen(G*t) )2 ) =
= √( 4C2 + F2G4*cos2(G*t) + F2G4*sen2(G*t) ) =
= √( 4C2 + F2G4*( cos2(G*t) + sen2(G*t) ) ) = √( 4C2 + F2G4*1 ) = √( 4C2 + F2G4 ), que es una expresión que no depende del tiempo.
Para la dirección de la aceleración, plantea la expresión de su vector unitario asociado:
u = ( 1/|a(t)| )*a(t), sustituyes, y queda:
u = ( 1 / √( 4C2 + F2G4 ) ) * < -2C , FG2*cos(Gt) , -FG2*sen(Gt) >, y observa que es una expresión que si depende del tiempo.
Y observa que el movimiento no es rectilíneo, porque una de las condiciones para que si lo sea es que el vector unitario asociado a la velocidad sea independiente del tiempo, y esta condición no se cumple (te dejo la tarea de verificarlo).
Espero haberte ayudado.
-
Hola estoy haciendo este problema y me he quedado atascada, alguien sabe como se podria hacer:
Sea una carga Q situada sobre el eje Y en el punto (0,3) y otra carga q situada sobre el eje X en el punto (4,0). ¿En que punto deberíamos situar una carga 2Q para que la fuerza total sobre la carga q se anule?
David
el 29/10/17¿Has visto este video? Campo eléctrico creado por dos cargas
A partir de ahí, se trata de que DESPUES DE IR A CLASE (ver los vídeos relacionados con vuestras dudas) enviéis dudas concretas, muy concretas. Y que nos enviéis también todo aquello que hayais conseguido hacer por vosotros mismos. Paso a paso, esté bien o mal. No solo el enunciado. De esa manera podremos saber vuestro nivel, en que podemos ayudaros, cuales son vuestros fallos.... Y el trabajo duro será el vuestro. Nos cuentas ¿ok? #nosvemosenclase ;-)
-
Hola, quería preguntarte como resolvería un problema de movimiento vertical de un cuerpo.
se lanza al suelo una pelota con velocidad inicial de 10m/s, ¿ que velocidad llevará cuando haya descendido 4 metros?
un saludo y gracias.
Jorge
el 28/10/17Seguramente en el curso en el que estés no plantees todavía la velocidad y la aceleración vectorialmente, pero, para futuros (y espero no equivocarme) voy a cambiarte el signo a la velocidad. En lugar de 10 m/s, voy a poner -10 m/s. Para entender esto simplemente necesitas establecer un eje OY y ver que, si la velocidad va hacia arriba, ésta será positiva y si va hacia abajo, ésta será negativa.
DATOS
Velocidad inicial = Vo = -10 m/s
hf = altura final = h - 4
Planteamos las ecuaciones del MRUA (nuestra aceleración será la gravedad y, al ir hacia abajo, será negativa):
e = e0 + Vo· t - 1/2 g · t2v = vo - g · t
Sacamos el tiempo que tarda en descender 4 metros de la ecuación del espacio (despejamos t):0 -4 = 0 + 10 · t - 1/2 · 9´8 · t2
-4 = 10t - 4´9t2
-4´9t2 + 10t + 4 = 0
Resolvemos la ecuación de 2º grado:
Soluciones: t =-0,34s y t = 2´38s, aunque descartamos la primera porque el tiempo no puede ser negativo.
Ahora sustituimos este tiempo en la ecuación de la velocidad:
v = vo - g · t
v = -10 - 9.8 · 2´38
v = - 33´324 m/s.
Tenemos una velocidad negativa justo por lo mismo de antes, al estar planteado vectorialmente, una velocidad que va hacia abajo, será negativa.
-
Tengo un ejercicio de física que no consigo sacar, ayudenme por favor, el ejercicio es el siguiente:
Un cubo que tiene lados de longitud L=0.30m se coloca con una esquina en el origen de coordenadas, orientado en sentido positivo de los ejes, en una zona donde existe un campo eléctrico no uniforme. Si el campo viene dado por: E=(-5.0xi + 3.0zk)(N/C)
Calcular: a) el flujo electrico a traves de cada una de las seis caras del cubo, b) determinar la carga electrica total dentro del cubo.
gracias de antemano.
-
Necesito que alguien me explique esto, perteneciente a la asignatura física general de primero de carrera de física:
Halle la desviación de una plomada con respecto a la dirección radial en un punto de la superficie de Júpiter
de latitud norte 37º sabiendo que el planeta tarda 9 horas y 51 minutos en dar una vuelta sobre su eje,
siendo su radio aproximadamente 7*10^4 km y la aceleración debida a la gravedad 26,5 m/s^2 .
Raúl RC
el 28/10/17Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
XenoPhenom
el 28/10/17Raúl RC
el 30/10/17xenophenom en unicoos abarcamos principalmente los contenidos generales abordados sobre los temas que David ha hecho en sus mas de 700 vídeos, los temas mas especificos universitarios son de una complejidad mayor que no tocamos porque el temario es infinito, lamento no poder ayudarte
-
Antonio Silvio Palmitano
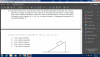
el 28/10/17Observa que el la dirección horizontal no actúan fuerzas exteriores al sistema bloque-cuña, ya que las componentes horizontales de la acción normal de la cuña sobre el bloque y de la reacción normal del bloque sobre la cuña, y del rozamiento que se ejercen mutuamente ambos cuerpos, provienen de fuerzas internas del sistema bloque-cuña, por lo tanto la componente horizontal de la cantidad de movimiento se conserva.
Luego, tienes dos instantes:
al inicio, tienes que tanto el bloque como la cuña están en reposo, por lo que la cantidad de movimiento del sistema es: pi = 0.
al final, tienes que el bloque y la cuña se desplazan, por lo que la cantidad de movimiento del sistema es: pf = Mc*vc + Mb*vb.
Luego, por conservación de la cantidad de movimiento en la dirección horizontal, tienes:
pf = pi, sustituyes, y queda:
Mc*vc + Mb*vb = 0, hacespasaje de término, y queda:
Mb*vb = - Mc*vc, haces pasaje de factor como divisor, y queda:
vb = - Mc*vc/Mb,
luego, reemplazas datos (observa que consideramos que el sentido hacia la derecha es positivo), queda:
vb = - 10*3/5 = - 30/5 = - 6 Kg*m/s,
por lo que tienes que la componente horizontal de la velocidad del bloque es 6 m/s hacia la izquierda.
Espero haberte ayudado.
-
 Hola, este es un problema con el que yo y mis compañeros tenemos muchas complicaciones para resolver, ya que es de los más complejos. Podrías ayudarnos a resolverso? Gracias 😄
Hola, este es un problema con el que yo y mis compañeros tenemos muchas complicaciones para resolver, ya que es de los más complejos. Podrías ayudarnos a resolverso? Gracias 😄Antonio Silvio Palmitano
el 27/10/17a)
Las superficies son planos perpendiculares al eje OZ, y sus ecuaciones quedan: -100*z = K
b)
Plantea el potencial en el punto inicial: V1 = V(1,3,2) = -100*2 + K = - 200 V + K.
Plantea el potencial en el punto final: V2 = V(2,0,4) = -100*4 + K = - 400 V + K.
Luego, el trabajo queda:
W12 = q*ΔV12 = q*(V1 - V2), sustituyes, y queda:
W = -5*10-6*( (-200 + K) - (-400 + K) ) = -5*10-6*(-200 + 400) = -5*10-6*200 = -1000*10-6 = -103*10-6= -10-3 J.
c)
Observa que el campo tiene la dirección del eje OZ, y su componente en esta dirección es negativa, por lo que tienes que la carga puntual se mueve paralelamente al eje coordenado OZ, con sentido negativo.
Espero haberte ayudado.
-
Hola.
En el problema anterior, el cual también he mandado resuelto, mi duda es: ¿por qué si la cant. De movimiento es constante existe trabajo? Se supone que si cant. De movimiento es constante, la sumatoria de fuerzas es nula, con lo cual si no existen fuerzas, no existirá trabajo, ¿no?
Muchas gracias.
Un saludo.
claudio taipe
el 28/10/17Según lo que puedo entender, se refiere a que la cantidad de movimiento de sistema es constante. Es decir que la cantidad de movimiento inicial del sistema debe ser igual a la cantidad de movimiento final del sistema. No se refiere a que la cantidad de movimiento de cada cuerpo es constante, sino del sistema formado por la cantidad de cuerpos que incluye el ejercicio.