-
Buenas tardes! No consigo hallar el proceso para llegar a esta fórmula del MRUA:
e= v0 . t + 1/2 a.t
El profesor utilizó un gráfico v-t pero no consigo entender lo.
Agradecería una respuesta pronto, ya que el examen es dentro de poco! Muchas gracias.
claudio taipe
el 1/11/17Para llegar a esa fórmula necesitas considerar la aceleración como constante.
a = dv/dt -> adt = dv -> ∫adt = ∫dv -> at = v - v0 , donde asumismo que el movimiento empieza desde un instante t=0 y con velocidad v=v0
despejando la velocidad: v= v0+at , ahora v=dr/dt -> vdt = dr
∫vdt = ∫dr -> ∫(v0 +at)dt=r - r0 -> v0t + 1/2 at2 =r -r0 , despejando r -> r= r0+v0t +1/2 at2 , si asumimos que para un instante t=0, la posición era r0=0
r=v0t +1/2 at2
-
Buenas tardes, no consigo encontrar la solución correcta a este problema:
Un satélite artificial de 250 kg se encuentra en una órbita circular alrededor de la Tierra a una altura de 500 km de su superficie. Si queremos transferirlo a una nueva órbita en la que su período de revolución sea tres veces mayor, calcula:
- La altura de esta nueva órbita y su velocidad lineal.
- La energía necesaria para realizar la transferencia entre ambas órbitas.
¡¡Muchísimas gracias!!
Antonio Silvio Palmitano
el 1/11/17Comienza por plantear la Segunda Ley de Newton:
G*MT*M/(RT+h)2 = M*acp,
haces pasaje de factor como divisor, y queda:
G*MT/(RT+h)2 = acp,
expresas a la aceleración centrípeta en función de la velocidad angular y el radio orbital, y queda:
G*MT/(RT+h)2 = ω2*(RT+h),
haces pasaje de factor como divisor, y queda:
G*MT/(RT+h)3 = ω2,
expresas a la velocidad angular en función del periodo orbital, y queda:
G*MT/(RT+h)3 = 4π2/T2,
haces pasaje de divisor como factor, y queda:
G*MT*T2/(RT+h)3 = 4π2,
haces pasaje de divisor como factor, y queda:
G*MT*T2 = 4π2*(RT+h)3 (1),
que es la ecuación que expresa la relación entre la altura orbital y el periodo orbital del satélite.
Luego, si denominas H a la nueva altura orbital, y denominas 3*T al nuevo periodo orbital, tienes para la relación entre estas dos cantidades:
G*MT*(3*T)2 = 4π2*(RT+H)3,
distribuyes la potencia en el último factor del primer miembro, ordenas factores, y queda:
9*G*MT*T2 = 4π2*(RT+H)3,
sustituyes la expresión señalada (1) en lugar de los tres factores remarcados, y queda:
9*4π2*(RT+h)3 = 4π2*(RT+H)3,
divides en ambos miembros por 4π2, y queda:
9**(RT+h)3 = (RT+H)3,
haces pasaje de potencia como raíz (observa que distribuimos la raíz en el primer miembro), y queda:
∛(9)*(RT+h) = RT+H,
haces pasaje de término, y queda:
∛(9)*(RT+h) - RT = H,
que es la expresión de la nueva altura orbital en función de la altura orbital inicial y del radio terrestre.
Espero haberte ayudado.
-
Se trata de una pregunta de MAS
Cuando la aceleración max se duplica, la energía mecánica también se debería duplicar de acuerdo con esto.
Sin embargi, teniendo enen cuenta que la fuerza elastica es conservativa podría hacerlo también usando la energía potencial. Pero me sale que se multiplicaría por 4 la energía mecánica. Por qué me sale esto? En cuál está el fallo y por qué?
Así que ¿Al duplicarse la a max, la energía mecánica qué hace? Y ¿Por qué?
Antonio Silvio Palmitano
el 1/11/17Recuerda la expresión del módulo de la aceleración máxima, en función de la amplitud de oscilación y del coeficiente angular:
aM = ω2*A (1).
Recuerda la expresión de la energía mecánica en función de la amplitud de oscilación, del coeficiente angular y de la masa del oscilador:
EM = (1/2)*M*ω2*A2 (2).
Luego, descompones el último factor como un producto en la expresión señalada (2), y queda:
EM = (1/2)*M*ω2*A*A,
luego sustituyes la expresión señalada (1) en lugar de los factores remarcados, y queda:
EM = (1/2)*M*aM*A (3),
que es la expresión de la energía mecánica en función de la masa del oscilador, del módulo de la aceleración máxima y de la amplitud de oscilación.
Luego, si duplicas el valor del módulo de la aceleración máxima, la nueva energía mecánica queda expresada:
EM1 = (1/2)*M*2*aM*A,
luego ordenas factores, y queda:
EM1 = 2*(1/2)*M*aM*A,
luego sustituyes la expresión señalada (3) en lugar de los factores remarcados, y queda:
EM1 = 2*EM,
por lo que tienes que la nueva energía mecánica es el doble de la energía mecánica inicial.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 1/11/17Recuerda la expresión del módulo de la aceleración máxima, en función de la amplitud de oscilación y del coeficiente angular:
aM = ω2*A, aquí sustituyes el primer factor por su expresión en función de la constante elástica y de la masa del oscilador, y queda:
aM = (k/M)*A, aquí haces pasaje de divisor como factor, y queda: M*aM = k*A,
haces pasaje de factor como divisor, y queda: M*aM/A = k (1).
Recuerda la expresión de la energía mecánica en función de la constante elástica y de la amplitud de oscilación:
EM = (1/2)*k*A2,
luego, sustituyes la expresión señalada (1), y queda:
EM = (1/2)*(M*aM/A)*A2,
luego simplificas, y queda:
EM = (1/2)*M*aM*A (2),
que es la expresión de la energía mecánica en función de la masa del oscilador, del módulo de la aceleración máxima y de la amplitud de oscilación.
Luego, si duplicas el módulo de la aceleración máxima, la nueva energía mecánica queda expresada:
EM1 = (1/2)*M*(2*aM)*A,
luego ordenas factores y queda:
EM1 = 2*(1/2)*M*aM*A,
luego, sustituyes los factores remarcados por la expresión señalada (2), y queda:
EM1 = 2*EM,
por lo que tienes que la nueva energía mecánica es el doble de la energía mecánica inicial.
Espero haberte ayudado.
-
hola
tengo una pregunta al entender una fórmula.
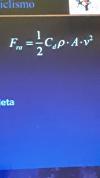
La pregunta es, si la Fra( fuerza de resistencia al aire) aumenta, que pasa con v^2 (velocidad al cuadrado).
V^2 aumenta el doble o disminuye el doble?
muchas gracias
Rodrigo Ivan Saez
el 3/11/17la v^2 aumenta : es como si multiplicaras Fra por un factor "a" si Fra aumenta en un factor de "a", para que se mantenga la igualdad, debes multiplicar el lado derecho por "a" tambien, y aislandolo de las demas constantes queda:
(a*Fra) = (1/2)Cd p (a*V^2)
obviamente si a>1 seria un aumento, si a<1 seria una disminucion
-
Buenas tardes, ¿cómo se realizaría este problema?
Se tienen dos masas mA=100 kg y mB=400 kg, colocadas en los puntos de coordenadas A(2, 0) y B(-1,0) medidas en metros.
- Calcula en qué punto de la recta que une ambas masas se anula el campo gravitatorio debido a ellas.
- Determina el trabajo necesario para trasladar un objeto de masa m=10 kg desde dicho punto al origen de coordenadas.
¡Muchísimas gracias!
-
Hola, el apartado C de este problema de campo eléctrico no me sale ¿Me podéis ayudar?
Las 2 cargas con una masa de 25 gramos de la figura están en el vacío i cuelgan de los extremos de un hilo de 1 metro de longitud cada una.En situación de equilibrio,cada hilo forma un angulo de 45º con la vertical.Haz un diagrama con las fuerzas que actúan y determina:
a)La fuerza con la que se repelen
b)El valor de las cargas q
c)El valor del angulo si las cargas se duplican
Antonio Silvio Palmitano
el 1/11/17Te ayudo con el planteo.
Tienes los datos:
M1 = M2 = 25 g = 0,025 Kg;
L = 1 m,
α = 45°.
Observa que la distancia que separa a los objetos es:
d = 2*L*senα = 2*1*sen(45°) = √(2) m.
Luego, observa que sobre cada una de los objetos actúan tres fuerzas, de las que indicamos sus módulos, direcciones y sentidos (consideramos g = 10 m/s2):
Pesos: P = M*g = 0,025*10 = 0,25 N, vertical y hacia abajo, para ambos objetos;
Tensiones: T, en la dirección de la cuerda correspondiente, hacia arriba, para ambos objetos;
Fuerza electrostática: F = k*q*q/d2 = k*q2/d2 = 9*109*q2/( √(2) )2 = 9*109*q2/2 = 4,5*109*q2 (en N),
horizontales, hacia la izquierda sobre el objeto señalado M1, y hacia la derecha sobre el objeto señalado M2.
Luego, plantea las componentes de las tensiones:
Tx = T*senα = T*sen(45°) = T*√(2)/2,
hacia la izquierda sobre el objeto señalado M1, y hacia la derecha sobre el objeto señalado M2.
Ty = T*cosα = T*cos(45°) = T*√(2)/2,
hacia arriba para ambos objetos.
Luego, aplicas la Primera Ley de Newton para el objeto señalada M2 y queda el sistema de ecuaciones:
F - Tx = 0
Ty - P = 0;
haces pasajes de términos, sustituyes expresiones, y queda:
4,5*109*q2 = T*√(2)/2
T*√(2)/2 = 0, 25;
y solo queda que resuelvas el sistema de ecuaciones con dos incógnitas, y tendrás el valor de las cargas, y con él podrás calcular el módulo de la fuerza electrostática.
Luego, aplicas la Primera Ley de Newton para el objeto señalada M1 y queda el sistema de ecuaciones:
-F + Tx = 0
Ty - P = 0;
y observa que tienes un sistema de ecuaciones equivalente al del paso anterior.
Luego, puedes repetir el procedimiento, porque tendrás los valores correspondientes a las cargas duplicadas.
Espero haberte ayudado.
-
¡NECESITO AYUDA!
Un tren, partiendo del reposo, acelera a un ritmo de 0.6 m/s2. Un pasajero de pié en el andén se encuentra a una distancia de 5 m de la puerta del tren cuando este comienza a moverse y comienza a correr hacia la puerta con una aceleración de 1.2 m/s2. ¿A qué distancia de la puerta se encontrará el pasajero después de 3 s?
A) 2.7 m
B) 5.4 m
C) 0.40 m
D) 2.3 m
E) 0.90 m
Me he quedado atascada, no se exactamente como igualar las ecuaciones del MRUA en este caso, agradecería mucho la ayuda. Un saludo! :)
Antonio Silvio Palmitano
el 31/10/17Plantea la ecuación para el punto correspondiente a la puerta del tren:
x = 5 + (1/2)*0,6*t2, resuelves el coeficiente, y queda:
x = 5 + 0,3*t2.
Para el pasajero:
x = (1/2)*1,2*t2, resuelves el coeficiente, y queda:
x = 0,6*t2.
Luego, plantea las posiciones a los tres segundos:
Para la puerta:
x = 5 + 0,3*32 = 5 + 2,7 = 7,7 m.
Para el pasajero:
x = 0,6*32 = 5,4 m.
Luego, plantea la diferencia entre las posiciones, y tendrás la distancia que separa al pasajero de la puerta, a los tres segundos:
d = 7,7 - 5,4 = 2,3 m.
Luego, tienes que la opción D es la respuesta correcta.
Espero haberte ayudado.
Jorge
el 31/10/17Veamos, tienes que el tren se desplaza con un MRUA y el pasajero, asimismo, con otro MRUA.
Planteas la ecuación del MRUA:
x = x0 + vo · t + 1/2 · a · t2
Sabiendo ahora que el tren parte del reposo, estableces un sistema de referencia para determinar la posición relativa. En este caso, el tren será mi eje de coordenadas.
Por tanto, tenemos que, para 3 segundos de desplazamiento.
Tren
x = 0 + 0 · 3 + 1/2 · 0´6 · 32
x = 2´7 metros se habrá desplazado.Pasajero
x = -5 + 0 · 3 + 1/2 · 1´2 · 32
x = 0´4 metros.(El desplazamiento total del pasajero NO serían estos 0´4 metros, ya que, mi posición inicial era -5. Si quisiéramos saber su desplazamiento deberíamos sumar estos 5 metros, quedando 5´4 m de desplazamiento del pasajero).
Efectúamos la resta entre ambas posiciones y obtendremos la distancia entre ambos.
2´7 - 0´4 = 2´3 metros se encontrará el pasajero de la puerta del tren.
-
cual seria la respuesta correcta?
Si para los vectores A y B diferentes del vector cero se cumple a la vez que A+B=C y UA+UB=D, se puede afirmar que:
a) D debe ser un vector unitario
b) los vectores C y D tienen necesariamente la misma dirección
c) los vectores A y B son componentes vectoriales del vector C
d) ninguna de las anteriores es correcta -
tengo otro problema que no lo entiendo?
1) se desea empernar una tuerca con su perno en una placa de acero si el agujero tiene un diámetro de 24 mm y el perno tiene 26 mm
¿Que temperatura necesita para lograr mi propósito?
Raúl RC
el 30/10/17Hola! Me encantaría ayudarte, pero no respondemos dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
Antonio Silvio Palmitano
el 31/10/17Puedes llamar α al coeficiente de dilatación lineal del acero cuyo valor tienes en tablas y libros, y tienes que 2α es su coeficiente de dilatación superficial.
Luego, tienes que el diámetro del agujero es: 24 mm = 2,4 cm, y que su área es: Sai = π*2,42/4 = 1,44π cm2.
Luego, tienes que el diámetro del perno es: 26 mm = 2,6 cm, y que su área es: Sp = π*2,62/4 = 1,69π cm2.
Observa que el diámetro final del agujero debe coincidir con el diámetro del perno.
Luego, si calientas, tienes que el agujero se dilata, y su variación de superficie queda:
ΔSa = Saf - Sai = 1,69π - 1,69π = 0,25π cm2.
Luego, plantea la ecuación de dilatación superficial:
Sai*2α*ΔT = ΔSa, haces pasajes de factores como divisores, y queda:
ΔT = ΔSa / (2α*Sai),
luego, reemplazas valores y tienes el aumento de temperatura.
Espero haberte ayudado.