Observa que tienes tres instantes importantes:

A: el bloque está en el punto más alto del plano inclinado A(0,h+s*senα);

B: el bloque está en el punto más bajo del plano inclinado, B(h*cosα,h);

C: el bloque está al nivel del suelo, en el punto C(p,0).

Luego, plantea el problema en dos etapas:

1°) 

Entre los puntos A y B:

EP_A = M*g*(h + s*senα), EC_A = 0,

EP_B = M*g*h, EC_B = (1/2)*M*V_B²;

luego puedes plantear conservación de la energía mecánica (despreciamos el rozamiento entre el bloque y el plano):

EP_B + EC_B = EP_A + EC_A, sustituyes expresiones, cancelas el término nulo y queda:

M*g*h + (1/2)*M*V_B² = M*g*(h + s*senα), ,multiplicas en todos los términos de la ecuación por 2/M y queda:

2*g*h + V_B² = 2*g*(h + s*senα),  distribuyes en el segundo miembro y queda:

2*g*h + V_B² = 2*g*h + 2*g*s*senα, haces pasaje de término (observa que tienes cancelación) y queda:

 V_B² = 2*g*s*senα, haces pasaje de potencia como raíz y queda:

V_B = √(2*g*s*senα), que es la expresión del módulo de la velocidad del bloque en el punto más bajo del plano inclinado,

y observa que su dirección es paralela al plano, y forma un ángulo α por debajo de la horizontal,

por lo que sus componentes son: v_Bx = v_B*cosα y v_By = - v_B*senα.

2°)

Entre los puntos B y C: Movimiento Parabólico (consideramos t = 0 cuando el bloque se encuentra en el punto B):

x = s*cosα +  v_B*cosα*t,

y = h - v_B*senα*t - (1/2)*g*t²,

v_x = v_B*cosα (constante),

v_y = - v_B*senα - g*t.

Luego plantea la condición de altura al nivel del suelo:

y = 0, sustituyes y queda:

h - v_B*senα*t - (1/2)*g*t² = 0, multiplicas en todos los términos de la ecuación pro - 2, ordenas términos y queda:

g*t² + 2*v_B*senα*t - 2h = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:

a) t = ( - 2*v_B - √(4*v_B²*sen²α + 8*g*h) ) / 2g, que es negativa y no tiene sentido para este problema;

b) t_C = ( - 2*v_B + √(4*v_B²*sen²α + 8*g*h) ) / 2g, que es positiva (observa que el el argumento de la raíz es mayor que (2*v_B)²),

y es el instante en que el bloque toca el suelo en el punto C.

Luego, sustituyes la expresión remarcada en las ecuaciones de posición y tienes:

x = s*cosα +  v_B*cosα*t_C = s*cosα +  v_B*cosα*( - 2*v_B + √(4*v_B²*sen²α + 8*g*h) ) / 2g = p,

y = h - v_B*senα*t - (1/2)*g*t² = te dejo la verificación = 0.

Luego, la distancia horizontal entre el punto C y el punto B queda:

L = p - s*cosα = v_B*cosα*( - 2*v_B + √(4*v_B²*sen²α + 8*g*h) ) / 2g;

y solo queda que sustituyas la expresión del módulo de la velocidad del bloque en el punto B.

Espero haberte ayudado.

Hola! Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

Recuerda la expresión del Módulo de Young:

E = (F/A) / (ΔL/L) = (F*L) / (A*ΔL), de donde puedes despejar:

E*A*ΔL / F = L.

Luego, observa que tienes todos los datos necesarios para calcular la longitud inicial de la varilla:

E =190*10⁹ = 19*10¹⁰ Pa,

A = π*d²/4 = π*(0,0060)²/4≅ 2,827*10^-5 m²,

ΔL = 73*10^-6 m,

F = 490 N,

L = a determinar (longitud inicial de la barra).

Luego, solo queda que hagas el cálculo.

Espero haberte ayudado.

¿?

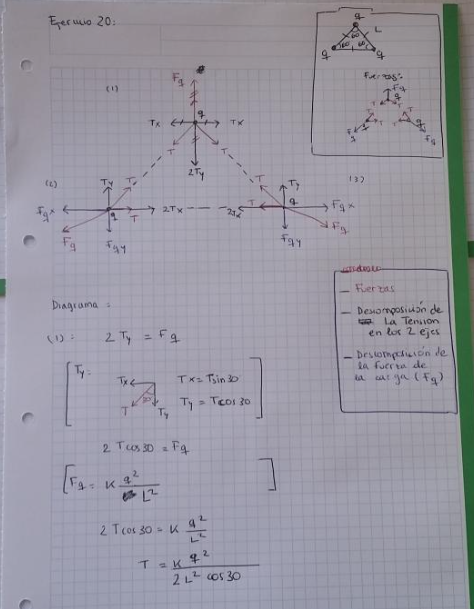
Observa la carga  q₁ que se encuentra en el vértice izquierdo más bajo del triángulo rectángulo,

y establece un sistema de referencia con origen en dicho vértice, eje OX horizontal hacia la izquierda y eje OY vertical hacia arriba.

Observa que sobre la carga actúan cuatro fuerzas, dos tensiones y dos de origen electrostático (que son repulsivas),

cuyos módulos, direcciones y sentidos son (llamamos q₂ a la carga del vértice más bajo a la derecha, y q₃ a la carga restante):

T₁₂ = T, horizontal hacia la derecha, cuyas componentes son:

T_12x = T,

T_12y = 0;

T₁₃ = T, inclinada 60° con respecto a la horizontal, hacia la derecha y hacia arriba, cuyas componentes son:

T_13x = T*cos(60°),

T_13y = T*sen(60°);

F₁₂ = F = k*q²/L², horizontal hacia la izquierda, cuyas componentes son:

F_12x = - F,

F_12y = 0;

F₁₃ = F = k*q²/L², inclinada 60° con respecto a la horizontal hacia la izquierda y hacia abajo, cuyas componentes son:

F_13x = - F*cos(60°),

F_13y = - F*sen(60°).

Luego, plantea las expresiones de las componentes de la tensión resultante:

T_Rx = T + T*cos(60°) = T + T*(1/2) = (3/2)*T,

T_Ry = 0 + T*sen(60°) = ( √(3)/2 )*T.

Luego, plantea las expresiones de las componenes de la fuerza electrostática resultante:

F_Rx = - F - F*cos(60°) = - F - F*(1/2) = - (32)*F,

F_Ry = 0 - F*sen(60°) = - ( √(3)/2 )*F.

Luego, plantea la condición de equilibrio (Primera Ley de Newton) en cada dirección:

T_Rx + F_Rx = 0

T_Ry + F_Ry = 0;

haces pasajes de términos en ambas ecuaciones y queda:

T_Rx = - F_Rx 

T_Ry = - F_Ry 

Luego sustituyes expresiones y queda:

(3/2)*T = +(3/2)*F

( √(3)/2 )*T = + ( √(3)/2 )*F,

haces pasajes de factores como divisores en ambas ecuaciones, y en en las dos llegas a la expresión:

T = F = k*q²/L².

Luego, recuerda que sen(30°) = 1/2, y puedes escribir:

T = 2*F*(1/2) = 2*F*sen(30°) = 2*k*q²/L²*sen(30°),

por lo que tienes que la opción (d) es la respuesta correcta.

Observa que por simetría, ya que las cargas son idénticas y están ubicadas en los vértices de un triángulo equilátero, tienes que las tensiones tienen módulos iguales en las tres cuerdas.

Espero haberte ayudado.

Establece un sistema de referencia usual, con origen en el punto de inicio del salto.

Luego, observa que tienes aceleración tanto en la dirección del eje OX como en la dirección del eje OY, ambas con sentido negativo con respecto a cada eje.

Luego, puedes plantear ecuaciones de Movimiento Rectilíneo Uniformemente Variado en ambas direcciones:

x = 8*cos(30°)*t - (1/2)*(g/4)*t²

y = 8*sen(30°)*t - (1/2)*g*t²

v_x = 8*cos(30°) - (g/4)*t

v_y = 8*sen(30°) - g*t.

Luego, reemplazas el valor del módulo de la aceleración gravitatoria, resuelves coeficientes y queda:

x = 8*cos(30°)*t - 1,25*t²

y = 8*sen(30°)*t - 5*t²

v_x = 8*cos(30°) - 2,5*t

v_y = 8*sen(30°) - 10*t.

Luego, puedes plantear la condición de altura máxima (v_y = 0, ya que el móvil "no sube ni baja" en dicho instante):

v_y = 0, sustituyes y queda:

8*sen(30°) - 10*t = 0, haces pasaje de término y queda:

- 10*t = - 8*sen(30°), haces pasaje de factor como divisor y queda:

t = 0,8*sen(30°) = 0,4 s, que es el instante en que el móvil alcanza su altura máxima;

luego reemplazas en la ecuación de alturas y queda:

y = 8*sen(30°)*0,4 - 5*(0,4)² = 1,6 - 0,8 = 0,8 m, que es la máxima altura que alcanza el móvil.

Luego, plantea la condición correspondiente a la altura del suelo:

y = 0, sustituyes y queda:

8*sen(30°)*t - 5*t² = 0, resuelves el coeficiente del primer término y queda:

4*t - 5*t² = 0, que es una ecuación polinómica cuadrática cuyas soluciones son:

a) t = 0, que es el instante de lanzamiento, cuya posición es:

x = 0,

y = 0;

b) t = 0,8 s, que es el instante en que el móvil vuelve al nivel del suelo, cuya posición es:

x = 8*cos(30°)*0,8 - 1,25*0,8² = 6,4*cos(30°) - 0,8 ≅ 5,543 - 0,8 = 4,743 m,

y = 8*sen(30°)*0,8 - 5*0,8² = 3,2 - 3,2 = 0.

Espero haberte ayudado.

Muchisimas gracias!!!

Una explicacion impresionante!

Álvaro sube el enunciado original sin pintadas, por favor. Un Saludo.

Listo Francisco, pura vida, saludos!...

Te lo envío hecho, Alba. Un Saludo.

La acción normal es siempre perpendicular a la superficie de apoyo, por lo tanto en este caso es perpendicular a la pared.

Espero haberte ayudado.

Sorry! Lamento de todo corazon no poder ayudarte, pero unicoos (por ahora) solo llega hasta bachiller con matemáticas, física y química. Tu duda se da en la "uni". Espero lo entiendas... Como a vecesel profe hace alguna excepción y además hay muchos enlaces de teoría y ejercicios resueltos, te recomiendo le eches un vistazo a los videos de momento de inercia

Momento de inercia

ya pero como habia videos sobre inercia pues...

Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya ha grabado como excepcion el profe. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas

Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)

ehh en realidad es un tema de 11° :/ 

Recuerda la expresión para la energía cinética:

EC = (1/2)*M*v²

y observa que es positiva, ya que los tres factores (1/2, masa y módulo de la velocidad al cuadrado) son positivos,

independientemente de la dirección de la velocidad.

Por lo tanto, tienes para las proposiciones del enunciado que los valores de verdad en orden son:

F V V F, por lo que la opción (b) es la respuesta correcta.

Espero haberte ayudado.