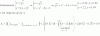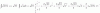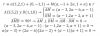-
luna
el 14/7/18Pueden ayudarme con el siguiente ejercicio
Antonio Silvio Palmitano
el 14/7/18Puedes comenzar por desarrollar cada término por separado:
(x2 + 3x - 1)*(x - 2) = x2*(x - 2) + 3x*(x - 2) - 1*(x - 2) = x3 - 2x2 + 3x2 - 6x - 1x + 2 = x3 + x2 - 7x + 2 = A;
3*(2x2 + 1) = 6x2 + 3 = B;
(x + 3)*(x2 + 1) = x*(x2 + 1) + 3*(x2 + 1) = x3 + x + 3x2 + 3 = x3 + 3x2 + x + 3 = C.
Luego, tienes para la expresión de tu enunciado:
(x2 + 3x - 1)*(x - 2) - 3*(2x2 + 1) + (x + 3)*(x2 + 1) =
sustituyes las expresiones señaladas (A) (B) (C), y queda:
= (x3 + x2 - 7x + 2) - (6x2 + 3) + (x3 + 3x2 + x + 3) =
distribuyes los agrupamientos de términos, y queda:
= x3 + x2 - 7x + 2 - 6x2 - 3 + x3 + 3x2 + x + 3 =
reduces términos semejantes, y queda:
= 2x3 - 2x2 - 6x + 2.
Espero haberte ayudado.
-
Usuario eliminado
el 14/7/18 -
Aimeé Sbraga Rodríguez
el 14/7/18Estimados Profes, me está saliendo "humo" de la cabeza. Estoy preparando un exámen final y no logro realizar un ejercicio de Integral Definida. Espero me puedan ayudar. La consigna es así:
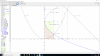
"Hallar el área de la región en el primer cuadrante que está acotada por las curvas (1) x=2√y ; (2) x=(y-1)² ; (3) y= -x +3. (Para los cálculos de los puntos a) y b) hallar intersecciones correspondientes).
a) Respecto al eje x; b) Respecto al eje y. c) Graficar"
He trabajado las ecuaciones en funcion de x y en función de y, pero mi problema es cuando quiero hallar a intersección de las curvas (1) y (2).
Pido una ayudita, quizás se me prenda una chispa!!!Saludos!!!!
-
Jesus
el 14/7/18
Como hacer el problema 4 por cambio de variable? No por integracion por partes, muchas gracias
Antonio Silvio Palmitano
el 14/7/18Tienes la integral:
I = ∫ √(10*x)*dx (1);
luego, plantea la sustitución (cambio de variable):
10*x = w2 (2), de donde tienes:
x = (1/10)*w2 (3), también tienes:
dx = (1/10)*2*w*dw = (1/5)*w*dw (4), y también tienes:
√(10*x) = w (5);
luego, sustituyes las expresiones señaladas (2) (4) en la expresión de la integral señalada (1), y queda:
I = ∫ √(w2)*(1/5)*w*dw,
simplificas el primer factor, extraes el factor constante, reduces factores, y queda:
I = (1/5)* ∫ w2*dw,
integras, y queda:
I = (1/5)*(1/3)*w3 + C,
reduces factores constantes, expresas a la potencia como un producto con un factor cuadrático, y queda:
I = (1/15)*w2*w + C;
luego, sustituyes las expresiones señaladas (2) (5), y queda:
I = (1/15)*(10*x)*√(10*x) + C,
reduces factores constantes en el primer término, y queda:
I = (2/3)*x*√(10*x) + C,
por lo que tienes que la opción señalada (C) es la respuesta correcta (observa que en la expresión señalada tienes que la constante arbitraria C toma el valor cero).
Espero haberte ayudado.
-
Bonifacio
el 14/7/18Hola! Tengo una pregunta de matemática de un ejercicio que no puedo resolver:
"Halle todos los puntos M pertenecientes a la recta r = α(1,2,1) + (0,−1,1) α ∈ R para que el triangulo AMB resulte rectangulo en M, siendo A = (3,5,2) y B = (1,1,0)."
Gracias!
-
XIME
el 13/7/18 -
XIME
el 13/7/18 -
Eduardo Leon
el 13/7/18Buenas, este ejercicio está bien?
Calcular el volumen generado por la curva y=4x-x^2 desde x=0 hasta x=4
Calcular el volumen si se rota la curva alrededor de y=6
A mi me quedó que el volumen=(1408/15)pi unidades cúbicas.
En el libro el resultado está como 2076/5 pi unidades cúbicas.
Gracias de antemano.
-
Eduardo Leon
el 13/7/18Buenas. Por favor ayúdenme a comprobar este ejercicio por favor.
Graficar y hallar el volumen generado al girar el área limitada por la parábola y^2=8x alrededor de la ordenada correspondiente al x=2
La guía de ejercicios dice que el resultado es igual a 256/15 pi unidades de volumen.
A mi me queda el resultado = 16/3 pi unidades cúbicas.
Gracias de antemano.
