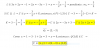-
Antonella
el 17/7/18
-
Judith Magni
el 16/7/18buenas!!!! nuevamente envío la consigna espero sea clara .
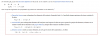
Determinar si el monoide (G,*) es grupo conmutativo, G={2,-2} y * es la adición habitual en Z
-
Jesus
el 16/7/18 -
Antonella
el 16/7/18Ya hice la grafica pero desde que punto tomo para la integral definida? o como seria la integral?
Antonio Silvio Palmitano
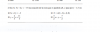
el 16/7/18Tienes la expresión del volumen:
V = π * ∫ ( (1/6)x3 + (1/2)(1/x )2 * dx,
desarrollas la suma de dos términos elevada al cuadrado, y queda:
V = π * ∫ ( (1/36)x6 + (1/6)x2 + (1/4)(1/x2) ) * dx,
integras (indicamos con Regla de Barrow que debes evaluar con Regla de Barrow entre x = 1 y x = 3), y queda:
V = π * [ (1/252)x7 + (1/18)x3 - (1/4)(1/x) ],
evalúas, y queda:
V = π * ( (243/28 + 3/2 - 1/12) - (1/252 + 1/18 + 1/4) ),
y solo queda completes el cálculo.
Espero haberte ayudado.
Antonella
el 16/7/18 -
Alvaro01
el 16/7/18Hola buenas tardes tengo dos dudas en el tema de vectores:
1.-EJERCICIO
Jorge realiza una excursión en tres etapas.En la primera se dirige hacia el este y anda 2km. En la segunda sigue andando 3km pero esta vez en dirección sudoeste.Finalmente,anda 4km en dirección norte ¿Qué distancia le separa del punto de partida al finalizarse la excursión?
2.-DUDA
No entiendo los ejercicios de hallar coordenadas en base {u,v} y expresar vectores en función de otros si alguien puede aconsejarme algún vídeo lo agradezco.
-
Mel
el 16/7/18 -
Alan Pariente
el 16/7/18Perdonen, me estoy iniciando en la lógica proposicional. He empezado a estudiar las proposiciones condicionales "si p entonces q" (p→q). He visto la tabla de verdad (FF→V),(FV→V),(VF→F),(VV→V).
No entiendo cuando dice (FV→V). El ejemplo del libro dice así. "Si ocho es un número par, entonces ocho es suma de dos números iguales". Entonces no logro entender esta proposición "Si ocho no es un número par, entonces ocho es suma de números iguales". Es decir la segunda parte de la proposición "ocho es suma de números iguales" depende de la primera " ocho es un número par" por eso se llama proposición consecuente. Es decir, es imposible que ocho no sea par y a la vez si sea suma de números iguales y por lo tanto la proposición condicional debería ser falsa.
¿Se me entiende? XD. A lo mejor con otro ejemplo podrías clarificarme las cosas.
-
García Barranco
el 16/7/18Hola menos días, les formulo el siguiente problema.
si C es la circunferencia con centro (-1,2) y radio =2. El punto(0,-1) está:
a) Fuera de C
b) Sobre C
C)Dentro de C
