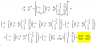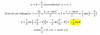-
Nico Tornero
el 1/6/18Hola, me podrían decir si el ejercicio esta bien resuelto? Creo que hice mal a igualar las ecuaciones a 5 y a 1, no entiendo como se hace desde ahí
(esta en azul porque puse algo que nada que ver)
Antonius Benedictus
el 1/6/18 -
Vivi
el 1/6/18 -
Susana Rubio
el 1/6/18 -
Samu
el 31/5/18 -
javier caballero
el 31/5/18Muy buenas, ¿estaría bien resuelto este ejercicio? Tengo dudas en si debería tener en cuenta algún otro punto de corte, por ejemplo entre alguna de las funciones con el eje x o si así basta con calcular los puntos de corte entre ambas. Muchas gracias de antemano. El enunciado es el siguiente:
.-Dadas las funciones f(x)= −x2 y g(x)=x2 −2x−4, calcula razonadamente el área del recinto cerrado limitado por sus gráficas.
-
anaespo
el 31/5/18 -
By SilviaAD
el 31/5/18Si alguien pudiera resolverme este examen se lo agradecería, no se ni por donde cogerlo 😭😭😭
Antonio Silvio Palmitano
el 31/5/181a)
Tienes la ecuación logarítmica:
2*log(x) - log(x-6) = 2 (observa que x debe tomar valores estrictamente mayores que seis),
aplicas la propiedad el logaritmo de una potencia en el primer término de la ecuación, y queda:
log(x2) - log(x-6) = 2,
aplicas la propiedad del logaritmo de una división en el primer miembro, y queda:
log( x2/(x-6) ) = 2,
tomas antilogaritmo en base diez en ambos miembros, y queda:
x2/(x-6) = 102,
resuelves el segundo miembro, multiplicas por (x-6) en ambos miembros, y queda:
x2 = 100*(x-6),
distribuyes el segundo miembro, restas 100x y sumas 600 en ambos miembros, y queda:
x2 - 100x + 600 = 0,
que es una ecuación polinómica cuadrática, cuyas soluciones son:
x1 = ( 100 - √(7600) )/2 ≅ 6,4110,
x2 = ( 100 + √(7600) )/2 ≅ 93,5890.
1b)
Tienes la ecuación exponencial:
52x - 30*5x + 125 = 0,
expresas al primer término como un cuadrado, y queda:
(5x)2 - 30*5x + 125 = 0,
aplicas la sustitución (cambio de incógnita): 5x = w (1) (observa que w toma valores estrictamente positivo), y queda:
w2 - 30*w + 125 = 0,
que es una ecuación polinómica cuadrática cuyas soluciones son:
w1 = 5,
reemplazas en la ecuación señalada (1), y queda:
5x = 5, de donde tienes: x1 = 1,
w2 = 25,
reemplazas en la ecuación señalada (1), y queda:
5x = 25, de donde tienes: x2 = 2.
Espero haberte ayudado.
Antonio Silvio Palmitano
el 31/5/182)
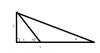
Puedes indicar con z a la altura del árbol, y con x a la primera distancia desde donde se lo observa. Luego, puedes plantear para el triángulo rectángulo más pequeño:
z/x = tan(42°), multiplicas por x en ambos miembros, y queda:
z = x*tan(42°) (1).
Luego, puedes indicar con y a una nueva distancia desde donde se observa el árbol, y puedes indicar con α al ángulo correspondiente. Luego, puedes plantear para el triángulo rectángulo más grande:
z/y = tanα, multiplicas por y en ambos miembros, y queda:
z = y*tanα (2).
Luego, igualas las expresiones señaladas (2) (1), y queda la ecuación:
y*tanα = x*tan(42°) (3).
Luego, tienes dos situaciones:
a)
y = 2*x, sustituyes en la ecuación señalada (3), y queda:
2*x*tanα = x*tan(42°), divides en ambos miembros por 2*x, y queda:
tanα = tan(42°)/2,
y solo queda que hagas uso de tu calculadora;
b)
y = 3*x, sustituyes en la ecuación señalada (3), y queda:
3*x*tanα = x*tan(42°), divides en ambos miembros por 3*x, y queda:
tanα = tan(42°)/3,
y solo queda que hagas uso de tu calculadora.
Espero haberte ayudado.
-
Susana Rubio
el 31/5/18 -
Iván
el 31/5/18Necesito ayuda con un problema de optimización:
-Se desea construir una caja de base cuadrada, con tapa y una capacidad de 80 dm3. Para la tapa y la superficie lateral se quiere utilizar un material que cuesta 2€/dm2 y para la base otro que cuesta 3€/dm2. Calcula las dimensiones de la caja para que su costo sea mínimo.
Mi problema viene a la hora de establecer las ecuaciones, una es fácil, la del volumen: x2 * y = 80
Pero la otra no sabría como hacerla, si alguien puede darme algún consejo para establecer las ecuaciones me vendría bien.
Gracias desde ya.
César
el 31/5/18
