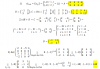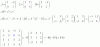-
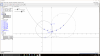
¿Alguna ayuda con este ejercicio? me piden determinar el lugar geométrico de los centros de una circunferencia tangente a la recta de ecuación y + 2 = 0 y que pasa por el punto (4, 4).
lo que hice fue un sistema donde (h,k) es el centro de las circunferencias luego (4-h)2+(4-k)2=r2 y (x-h)2+(-2-k)2=r2 ya que la distancia del punto 4,4 al centro es el radio y la distancia del centro a la recta es el radio también no se si estará bien, no se me ocurre nada mas que hacer
César
el 3/8/17 -
Antonius Benedictus
el 3/8/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
-
Antonius Benedictus
el 3/8/17¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que lo entiendas.
Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).
Victor
el 3/8/17Lo he hecho con δ1= 1 y me da igual que a ti. Pero al hacer una comprobación con entornos me da error. En un video de youtube dicen que cuando la función tiene asíntota como esta hay que coger δ1 = 1\2 ΙX0-aI "a" siendo la asíntota, en este caso -3/4. Así queda δ1= 1/8 y al hacer la comprobación me sale correcto.
-
Antonio Silvio Palmitano
el 3/8/17Puedes denominar P(x,y) al punto extremo del vector AP, que queda expresado:
AP = < x-2 , y-3 >, luego tienes en el enunciado que las componentes del vector son: AP = < 10 , 6 >,
luego igualas componente a componente y tienes el sistema de ecuaciones:
x - 2 = 10, de esta ecuación despejas: x = 12
y - 3 = 6, de esta ecuación despejas: y = 9,
y tienes que las coordenadas del punto extremo del vector AP son: P(12,9).
Luego, tienes que los puntos P0(-1,3) y P(12,9) pertenecen a la recta, por lo que planteas para su pendiente:
m = (9-3) / ( 12-(-1) ) = 6/13,
y su ecuación cartesiana, con el punto P0(-1,3) como punto de referencia, queda:
y - 3 = (6/13)*( x - (-1) ), distribuyes en el segundo miembro y queda:
y - 3 = (6/13)*x + 6/13, haces pasaje de término, reduces términos semejantes y queda:
y = (6/13)*x + 45/13, que es la ecuación cartesiana explícita de la recta.
Espero haberte ayudado.
Guillem De La Calle Vicente
el 4/8/17Antonio Silvio Palmitano
el 5/8/17Muchas gracias colega Guillem por tu observación. Vamos con el desarrollo corregido, aunque es seguro que Laura ya lo ha hecho.
Puedes denominar P(x,y) al punto extremo del vector AP, que queda expresado:
AP = < x-2 , y-3 >, luego tienes en el enunciado que las componentes del vector son: AP = < 10 , - 6 >,
luego igualas componente a componente y tienes el sistema de ecuaciones:
x - 2 = 10, de esta ecuación despejas: x = 12
y - 3 = - 6, de esta ecuación despejas: y = - 3,
y tienes que las coordenadas del punto extremo del vector AP son: P(12,- 3).
Luego, tienes que los puntos P0(-1,3) y P(12,- 3) pertenecen a la recta, por lo que planteas para su pendiente:
m = (-3-3) / ( 12-(-1) ) = - 6/13,
y su ecuación cartesiana, con el punto P0(-1,3) como punto de referencia, queda:
y - 3 = - (6/13)*( x - (-1) ), distribuyes en el segundo miembro y queda:
y - 3 = - (6/13)*x - 6/13, haces pasaje de término, reduces términos semejantes y queda:
y = - (6/13)*x + 33/13, que es la ecuación cartesiana explícita de la recta.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 2/8/17(a)
Plantea el módulo del vector u:
|u| = √(12 + (-2)2 +32) = √(1 + 4 + 9) = √(14).
(b)
Comienza por calcular el modulo del vector V:
|v| = √(12 +12 +12) = √(1 + 1 + 1) = V(3),
luego plantea al vector unitario correspondiente como el vector dividido por su propio módulo:
V = v/|v| = < 1 , 1 , 1 > / V(3) = < 1/V(3) , 1/V(3) , 1/V(3) >.
(c)
Comienza por plantear el producto escalar entre el vector v y el vector u en función de las componentes de los vectores:
v • u = < 1 , 1 , 1 > • < 1 , -2 , 3 > = 1*1 + 1*(-2) + 1*3 = 1 - 2 + 3 = 2;
luego plantea el producto escalar entre el vector v y el vector u en función de los módulos de los vectores y del ángulo determinado por ellos:
v • u = |v|*|u|*cosα = √(14)*√(3)*cosα = √(14*3)*cosα = √(42)*cosα,
luego igualas las expresiones del producto escalar y queda:
√(42)*cosα = 2,
hace pasaje de factor como divisor y queda:
cosα = 2/√(42),
luego compones en ambos miembros con la función inversa del coseno y queda:
α ≅ 72,02°.
Espero haberte ayudado.
-
Hola,
Me gustaría saber como resuelve esta ecuación:
senx + i cosx= (1- i√3)/2
La solución sería 5π/6 + 2kπ , pero no se como llegar a ella.
Alguien sabría como es el procedimiento ?
Muchas gracias!!
Antonio Silvio Palmitano
el 2/8/17Comienza por distribuir el denominador en el segundo miembro, lo haces y queda:
senx + i*cosx = 1/2 - i*√(3)/2,
luego igualas los términos reales en una ecuación, y los términos imaginarios en otra ecuación y queda el sistema:
senx = 1/2
i*cosx = - i*√(3)/2,
haces pasaje de factor imaginario como divisor en la segunda ecuación y queda:
senx = 1/2 (observa que x pertenece al primer cuadrante o al segundo cuadrante)
cosx = - √(3)/2 (observa que x pertenece al segundo cuadrante o al tercer cuadrante),
luego, divides miembro a miembro entre las dos ecuaciones y queda:
tanx = - 1/√(3),
luego compones en ambos miembros con la función inversa de la tangente (observa que debes corregir el valor que te devuelve tu calculadora porque el valor de la incógnita x corresponde a un ángulo del segundo cuadrante) y queda:
x = - 30° + 180° = 150° = 150π/180 = 5π/6 rad.
Espero haberte ayudado.
-
hola, quería saber si este ejercicio esta hecho correctamente,así esta hecho, lo hice y me da 32. gracias.
Un consejo formado por alicia, berta, carlos, dario, elena y francisco debe elegir un presidente, un secretario y un tesorero.
¿De cuantas maneras puede hacerse si berta es presidente o carlos es secretario?
Si berta es presidente hay 20 maneras de ocupar los otros 2 cargos. También, siendo carlos secretario hay 20 maneras de ocupar los otros cargos. pero en este caso el conjunto de posibilidades en las que berta es presidente y el conjunto de posibilidades en las que carlos es secretario no son disjuntos. Las asignaciones de cargos que tienen a berta como presidente y a carlos como secretario pertenecen a ambos conjuntos ( estas son 4 posibilidades). Así que el numero de maneras de elegir presidente, secretario y tesorero, con berta como presidente o con carlos como secretario es: 20+20-4=36.Antonio Silvio Palmitano
el 2/8/17Vas muy bien, pero observa que puedes plantear tres opciones disjuntas:
1)
Observa que las elecciones posibles con B presidente, sin que C sea secretario son:
BAC BAD BDA BAE BEA BAF BFA BDC BEC BFC BDE BED BDF BFD BEF BFE,
en total: N1 = 1*4*4 =16 maneras;
2)
observa que las elecciones posibles con C secretario, sin que B sea presidente son:
ACB ACD DAC ACE ECA ACF FCA DCB ECB FCB DCE ECD DCF FCD ECF FCE,
en total: N2 = 4*1*4 = 16 maneras;
3)
observa que las elecciones posibles con B presidente y C secretario son:
BCA BCD BCE BCF,
en total: N3 = 1*1*4 = 4 maneras.
Luego, por el principio de adición, tienes en total:
N = N1 + N2 + N3 = 16 + 16 + 4 = 36 maneras,
para elegir consejos con B como presidente o C comos secretario.
Espero haberte ayudado.