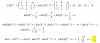Lo que te dice que evaluando el polinomio en -2 ( o sea reemplazando las x por -2 )  te tiene que dar 4

Si queres que lo resuelva decime

marcos por favor resuelve , 

Nelson ¿de donde sale el 5?

Coincido con Victor, da -4

Perdón que lo moleste con otro ejercicio.

En el ejercicio, me pide hallar ecuación vectorial del plano que es paralelo al plano 2x-y+3z=1 y pasa por el punto (-1;-2;3). Muchas gracias.

Muchísimas gracias!

El enunciado no esta muy claro, pero mas o menos lo que se me ocurre es hacer una regla de tres.  

100% --------- $100

3% --------------$ x

Entonces es (3* 100)/100. = $3

Entonces por cada mes tiene una ganancias de $3. 

Otra forma de interpretar el problema (segun mi) es la siguiente: 

Que todos los meses deposita $100 y obtiene por eso $3 pesos cada mes. Luego retira los 103 y así cada mes. 

Entonces de ganancia total en un año es 3*12 = $36

Tema: Interés simple

Concepto: Monto

En las primeras 3 diapositivas tienes toda la teoría y fórmulas necesarias para este ejercicio

https://issuu.com/franckh/docs/antolog_a_matem_ticas_financieras_copia

Una persona deposita mensualmente una cuota de $100 a una tasa del 3% mensual. Calcular aproximadamente el capital obtenido.

M=100*[1+(0.03/1)] = 100(1+0.03) = 100*1.03 = 103 euros

Puede ser que la interpretación 3) sea la correcta porque veo "sospechoso" que te digan que calcules "aproximadamente" un resultado que sale tan exacto como son 103.00 euros:

1) La forma en que lo interpreté ayer es de interés simple tomando como periodo un mes 

2) La otra forma que apuntó Marcos es una suma del interés generado mes a mes durante un año (interés simple también)

3) Te propongo lo hagas con una pequeña modificación en tu enunciado:

Una persona tiene en una cuenta de ahorro $100 a una tasa fija del 3% mensual. Calcular aproximadamente el capital obtenido al cabo de un año

(resuélvelo con los apuntes del link que te envié, te viene la fórmula del interés compuesto)

Resultaría:

Al finalizar el primer mes: 100*1.03= 103euros

Al finalizar el segundo mes: 103*1.03= 106.09euros

https://www.unicoos.com/video/matematicas/1-bachiller/matematica-financiera/interes-simple-y-compuesto/interes-simple-y-compuesto

(x+1)²+y²≤4   ------>     [x-(-1)]²+[y-0]²≤2²  ---->  Abarca la región interior del círculo y el propio círculo de radio 2, y centro (-1,0)

x²+(y-2)²≤4   ------>     [x-0]²+[y-2]²≤2²  ---->  Abarca la región interior del círculo y el propio círculo de radio 2, y centro (0,2)

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

¡Hola! Nos encantaría ayudarte, pero no solemos responder dudas universitarias que no tengan que ver específicamente con los vídeos que David ha grabado como excepción. O de otras asignaturas que no sean Matemáticas, Física y Química. Lo sentimos de corazón… Esperamos que  lo entiendas.

Ojalá algún unicoo universitario se anime a ayudarte (de hecho, lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros).

Observa que tienes matrices de orden n = 3.

Luego, recuerda algunas de las propiedades de los determinantes:

1) d(X*Y) = d(X)*d(Y) (determinante de un producto de matrices),

2) d(Xⁿ) = ( d(X) )ⁿ (determinante de una potencia de una matriz),

3) d(I) = 1 (determinante de la matriz identidad,

4) d(X^-1) = 1/d(X) (determinante de la matriz inversa), 

5) d(X^T) = d(X) (determinante de la matriz traspuesta).

Luego, tienes los datos del enunciado

d(B^T) = 1/4, luego aplicas la propiedad (5) y tienes:

d(B) = 1/4 (*);

luego tienes la matriz (AB)^-1, calculas su determinante (te dejo la tarea) y queda:

d( (A*B)^-1 ) = - 8, luego aplicas la propiedad señalada (4) y tienes:

1/d(A*B) = - 8, haces pasaje de divisor como factor y queda:

1 = - 8*d(A*B), haces pasajes de términos y queda:

8*d(A*B) = - 1, haces pasaje de factor como divisor y queda:

d(A*B) = - 1/8, luego aplicas la propiedad señalada (1) y tienes:

d(A)*d(B) = - 1/8, luego sustituyes el valor remarcado y señalada (*) y queda:

d(A)*(1/4) = - 1/8, multiplicas en ambos miembros de la ecuación por 4 y queda:

d(A) = - 1/2 (**).

Luego, tienes la expresión cuyo valor piden calcular:

d(I*A³*B^-1) = aplicas la propiedad señalada (1) y queda:

= d(I)*d(A³)*d(B^-1) = aplicas las propiedades señaladas (3) (2) (4) y queda:

= 1 * ( d(A) )³ * 1/d(B) = reemplazas los valores remarcados y señalados (*) (**) y queda:

= 1 * (-1/2)³ * 1/(1/4) = resuelves los dos últimos factores y queda:

= 1*(-1/8)*4 = - 1/2.

Espero haberte ayudado.

Para empezar no se que te piden, creeria que es hallar todas las corrientes y voltajes. Inicia con V7 que es igual al de la fuente de voltaje, es decir 16v, ya que estan en paralelo. Con esto conoces el voltaje en la resistencia y puedes hallar i7. Con esta corriente y teniendo en cuenta la fuente de corriente de 0.5A puedes  hallar la corriente que baja por la fuente de 16v. Igualmente es facil hallar i2 ya que las otras dos corrientes que entran al nodo son conocidas, las de la fuente de 0.4 y 0.3 A. Si hallas i2 puedes hallar i5 ya que en el nodo de donde sale i5 estan involucradas i2 y la fuente de 0.5A. Ya con esto hallas las otras corrientes y aplicas ley de voltajes de kirchhoff para hallar los voltajes.

Puedes plantear la sustitución (cambio de variable):

x = - w, y observa que w tiende a +infinito cuando x tiende a -infinito,

luego sustituyes y el límite queda:

Lím(w→+∞) 5*( ln( (-w)² + 4(-w) - 5 ) ) - 4(-w) + 3 =

resuelves signos en todos los términos que dependen de w y queda:

= Lím(w→+∞) 5*( ln(w² - 4w - 5) ) + 4w + 3 =

extraes factor común w² en el argumento del logaritmo y queda:

= Lím(w→+∞) 5*( ln( w²(1 - 4/w - 5/w²) ) ) + 4w + 3 = +∞.

observa que el argumento del logaritmo tiende a +infinito, por lo que el término logarítmico también tiende a + infinito, y también observa que 4w tiende a +infinito.

Espero haberte ayudado.

pero, si sustituyo x->-inf sigue la indeter +inf (por ln(x^2))-inf(por -4x)?

Observas correctamente que el primer término tiende a +infinito, porque el logaritmo tiende a +infinito.

Pero observa que el segundo término (- 4*x) "tiende a - 4 * -infinito, que corresponde a +infinito".

Por lo tanto, tienes que la expresión tiende a "+infinito +infinito +3, que corresponde a +infinito".

Espero haberte ayudado.

pero la función en realidad tiende a -inf cuando x tiende a -inf

x²+y²>1  ---->    x²+y²>1²

Abarca la toda la región que se encuentra FUERA de la circunferencia trazada desde (0,0) con radio uno o dicho de una forma complementaria: se excluye sólo el "interior" de la circunferencia y el área de la propia circunscripción de ésta de la región definida en todo ℛ

 x²+y²<4   --->  x²+y²<2²

Abarca la toda la región que se encuentra DENTRO de la circunferencia trazada desde (0,0) con radio 2 o dicho de una forma complementaria: se incluye sólo el "interior" de la circunferencia y se excluye de su definición en  el área de la propia circunscripción de ésta y las restantes regiones de ℛ