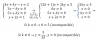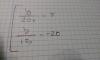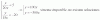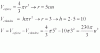-
Muy buenas, podrían ayudarme también a plantear simplemente la función de los ingresos de este ejercicio? 2A
Antonio Silvio Palmitano
el 7/6/17Puedes plantear una tabla de valores: precio de la entrada - cantidad de espectadores - ingreso,
en la que señalamos con x al aumento genérico de la entrada expresado en euros
P C Y
4 100 4*100 = 400 (ingreso con entrada sin aumento)
4+1 100-10*1 (4+1)*(100-10*1) (ingreso con entrada aumentada 1 euro)
4+2 100-10*2 (4+2)*(100-10*2) (ingreso con entrada aumentada 2 euros)
4+3 100-10*3 (4+3)*(100-10*3) (ingreso con entrada aumentada 3 euros)
...
4+x 100-10*x (4+x)*(100-10*x) (ingreso con entrada aumentada x euros).
Luego, la expresión del ingreso en función del aumento de la entrada queda:
Y(x) = (4 + x)*(100 - 10*x) = 400 - 40*x + 100*x - 10*x2= 400 + 60*x - 10*x2.
Luego, plantea la expresión de la función derivada y queda:
Y ' (x) = 60 - 20*x,
luego plantea la condición de punto crítico (posible máximo o posible mínimo):
Y ' (x) = 0, sustituyes y quea:
60 - 20*x = 0, haces pasaje de término y queda:
- 20*x = - 60, haces pasaje de factor como divisor y queda:
x = 3 euros;
luego, la cantidad de espectadores queda:
C = 100 - 10*3 = 100 - 30 = 70;
y el ingreso correspondiente queda:
Y(3) = 400 + 60*3 - 10*32 = 400 + 180 - 90 = 490 euros.
Puedes evaluar para otros valores de x, uno mayor que 3 y uno menor que 3, para corroborar que el ingreso es máximo para un aumento de 3 euros:
Y(2) = 400 + 60*2 - 10*22 = 400 + 120 - 40 = 480 euros;
Y(4) = 400 + 60*4 - 10*42 = 400 + 240 - 160 = 480 euros.
Espero haberte ayudado.
-
Antonio Silvio Palmitano
el 7/6/17Has planteado correctamente todo, y luego te ha quedado el sistema de dos ecuaciones con dos incógnitas:
2a - 2b = 16
3a - 3b = 24
divides por 2 en todos los términos de la primera ecuación y queda:
a - b = 8, haces pasaje de término y queda:
a = b + 8,
luego, sustituyes en la segunda ecuación y queda:
3(b + 8) - 3b = 24, distribuyes el primer término y queda:
3b + 24 - 3b = 24, cancelas términos opuestos en el primer miembro y queda:
24 = 24,
que es una identidad verdadera, por lo que tienes que el sistema de ecuaciones admite infinitas soluciones, que quedan expresadas en la forma:
a = b + 8,
b ∈ R.
Por lo tanto, la expresión de la matriz incógnita queda:
X =
b+8 2
-3 b,
con b perteneciente al conjunto de los números reales.
Espero haberte ayudado
-
Hola Unicoos!!. Me pueden decir si plantie bien el siguiente ejercicio de integrales por favor?
La consigna es hallar el area limitada por las siguientes curvas y=2x+3; y= - x +5; x=-3 y x=3
La integral la plantie así: Muchas gracias
Antonio Silvio Palmitano
el 7/6/17Observa que las rectas cuyas ecuaciones son:
y = 2x + 3
y = -x + 5
se cortan en el punto de coordenadas: A(2/3,13/3),
cuya abscisa (x = 2/3) pertenece al intervalo limitado por x = - 3 y x = 3.
Luego, haz un gráfico, y verás que la región está dividida en dos triángulos,
y para el triángulo de la izquierda tenemos que la segunda recta es "más alta" que la primera,
y para el triángulo de la derecha tenemos que la primera recta es "más alta" que la segund.
Luego, llamamos Ai al área del triángulo de la derecha, y llamamos Ad al área del triángulo de la derecha,
por lo que planteamos para el área de la región:
AR = Ai + Ad.
Luego, planteamos las áreas de los triángulos por separado:
Ai = ∫ ( (-x+5) - (2x+3) )dx = ∫ (-3x + 2)dx, para evaluar con Regla de Barrow entre - 3 y 2/3;
Ad = ∫ ( (2x+3) - (-x+5) )dx = ∫ (3x - 2)dx, para evaluar con Regla de Barrow entre 2/3 y 3.
Luego, puedes resolver las integrales y sumar sus resultados para concluir la tarea.
Espero haberte ayudado.
-
Hola, este es un problema de mates de universidad, pero David ha tocado este tema:
Podrían ayudarme con este ejercicio?
Resolver el problema de valor inicial y' +(x^3)y = 4x^3 en y(0) = -1
Me harian un gran favor!
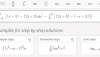
Lo que se es que primero hay que poner las y en un lado y las x en el otro. : queda asi: ∫dy/(4-y) = ∫(x^3)dx
Despues lo integro y queda: y/4 - ln(y) = (x^4)/4
Pero no se hacer mas...
Antonio Silvio Palmitano
el 7/6/17Tienes la ecuación diferencial lineal, de primer orden y primer grado, con la condición inicial y(0) = - 1:
y ' + x3y = 4x3, luego has planteado correctamente la separación de variables:
haces pasaje de término y queda:
y ' = 4x3 - x3y, extraes factor común, escribes a la derivada como cociente entre diferenciales, y queda:
dy/dx = x3(4 - y), haces pasajes de divisor y de factor y queda:
dy/(4 - y) = x3dx, luego integras en ambos miembros y queda (atención con el primer miembro):
- ln|4 - y| = x4/4 + C, que es una forma implícita de la solución general de la ecuación diferencial,
luego, evalúas para x = 0 e y = - 1 y queda:
- ln(5) = 0 + C, de donde tienes: - ln(5) = C,
luego reemplazas en la expresión de la solución general y queda:
- ln|4 - y| = x4/4 - ln(5), que es una forma implícita de la solución particular de la ecuación diferencial,
con la condición inicial: x = 0 e y = - 1.
Espero haberte ayudado.
-
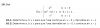
 Tengo dos dudas la primera es que cuando saco el f(0+) me da "a(0)^2 +b(0) + c = e^3(0) que es equivalente a c=1" pero a usted le da c=0 y mi segunda duda es que el x^3 lo deriva a 3x^2 (perfecto hasta aqui) pero lo vuelve a derivar a 6x y no entiendo porque (osea el método que usa para determinar que debe derivar dos veces).
Tengo dos dudas la primera es que cuando saco el f(0+) me da "a(0)^2 +b(0) + c = e^3(0) que es equivalente a c=1" pero a usted le da c=0 y mi segunda duda es que el x^3 lo deriva a 3x^2 (perfecto hasta aqui) pero lo vuelve a derivar a 6x y no entiendo porque (osea el método que usa para determinar que debe derivar dos veces).Antonio Silvio Palmitano
el 7/6/17Recuerda que una función debe ser continua en un punto, porque es condición necesaria para que sea derivable en dicho punto.
Observa que la expresión de la función derivada queda planteada:
f ' (x) =
3e3x x > 0
a determinar x = 0
2ax + b 0 < x < 1
a determinar x = 1
3x2 x > 1
Luego tienes los ejercicios:
10.1.
Debes plantear:
a) continuidad en x = 0,
b) continuidad en x = 1,
c) derivabilidad en x = 1 (para este último planteo, puedes derivar en cada rama y tomar los límites laterales correspondientes para x tendiendo a 1, que deben coincidir);
haces los planteos (te dejo la tarea) y queda una ecuación para cada caso:
c = 1 (a)
a + b + c = 1 (b)
2a + b = 3 (c);
luego resuelves el sistema de ecuaciones y tienes la solución:
a = 3, b = - 3, c = 1.
10.2.
a) continuidad en x = 0,
b) continuidad en x = 1,
c) derivabilidad en x = 0 (para este último planteo, puedes derivar en cada rama y tomar los límites laterales correspondientes para x tendiendo a 1, que deben coincidir);
haces los planteos (te dejo la tarea) y queda una ecuación para cada caso:
c = 1 (a)
a + b + c = 1 (b)
b = 3 (c);
luego resuelves el sistema de ecuaciones y tienes la solución:
a = - 3, b = 3, c = 1.
Espero haberte ayudado.
-
Buenos días como me puedo aprender las funciones a trozos en día y medio ? Es posible? Tengo el examen en nada y no le di cuenta de repasarlo antes y sin 2 puntos en el examen por favor me pueden ayudar es importante que apruebe .mil gracias y siento las molestias
César
el 7/6/17