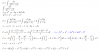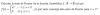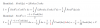-
Daiana Zapata
el 8/6/17Hola. Me pueden ayudar por favor? No se como seguirlo. Tengo q resolverlo por sustitución de modo que las rqicees queden enteras.
Antonio Silvio Palmitano
el 8/6/17Vas bien con los planteos.
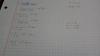
Observa que en tu segunda sustitución (cambio de variable) tienes:
u = 1 - t, de donde puedes despejar: t = 1 - u, y también: dt = - du.
Luego, sustituyes y la integral queda:
I = 6 ∫ ( t3/(1- t) ) dt = 6 ∫ ( (1-u)3/u ) (-du) = - 6 ∫ ( (1 - 3u + 3u2 - u3)/u ) du = - 6 ∫ (1/u - 3 + 3u - u2) du = - 6 ( ln|u| - 3u + 3u2/2 - u3/3 ) + C.
Luego, solo queda que vuelvas a sustituir, para expresar la solución en función de la variable independiente x.
Espero haberte ayudado.
Neofito 007
el 8/6/17Lo que he resuelto arriba está bien (salvo un detalle menor) pero no corresponde a tu ejercicio , aunque sólo difiere al final en el cambio de variable.
En tu ejercicio por la forma como lo haces seguro no vas a obtener lo que ponen en tu respuesta . Acá hay un asunto muy importante que corresponde a la teoría ,
cuando se calcula la antiderivada lo que se obtiene en sí es una familia de funciones cuya derivada es la función integrando (por eso se agrega al final la constante)
Entonces dependiendo del cambio de variable se pueden obtener expresiones diferentes para una misma antiderivada , si estas son correctas entonces se deben
diferenciar en una constante.
Por ejemplo ∫2SenxCosxdx =(Senx)^2 +C1 = - (Cosx)^2 +C2 = - (1/2)Cos2x +C3
Adjunto solución esta vez sí de tu ejercicio , calculando de 2 formas : como lo estás planteando y sin un segundo cambio de variable , fíjate el detalle de las expresiones diferentes
A modo de comprobación pongo links de Wolfram Alpha
Comprobación del primer resultado https://goo.gl/HIYsHn
Comprobación del segundo resultado https://goo.gl/lN4kJ4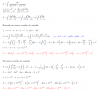
-
Gerardo Lazaro
el 8/6/17Necesito ayuda en estos dos problemas de como resolverlo,me urge
Antonio Silvio Palmitano
el 8/6/171)
Si consideras t = 1 para el año 2001, tienes que para el año 2006 el valor correspondiente es t = 6,
y la venta anual queda:
S = 150000 + 3000*6 = 150000 + 18000 = 168000 dólares.
Observa que para valor de t que quieras sustituir existe un único valor de S, por lo que tienes que S es una función de t.
2)
Tienes la expresión de la función:
f(n) = (10/9)n(12 - n) = (40/3)n - (10/9)n2,
luego planteas la expresión de la función derivada y queda:
f ' (n) = 40/3 - (20/9)n,
luego planteas la condición de punto crítico (posible máximo o posible mínimo):
f ' (n) = 0, sustituyes la expresión del primer miembro y queda:
40/3 - (20/9)n = 0, multiplicas en todos los términos de la ecuación por - (9/20), simplificas y queda:
- 6 + n = 0, haces pasaje de término y queda:
n = 6.
Luego, puedes probar que corresponde a un máximo de la función evaluándola para un valor menor y otro mayor que n = 6:
f(5) = (10/9)*5*(12 - 5) = (10/9)*5*7 ≅ 38,8889, que corresponde a 38889 familias;
f(6) = (10/9)*6*(12 - 6) = (10/9)*6*6 = 40, que corresponde a 40000 familias;
f(7) = (10/9)*7*(12 - 7) = (10/9*7*5 ≅ 38,8889, que corresponde a 38889 familias.
Por lo tanto, la cantidad máximas de familias que utilizarán el producto es cuarenta mil, y lo harán a los seis meses de lanzado el producto.
Espero haberte ayudado.
-
Móny Fernández
el 8/6/17
-
lbp_14
el 8/6/17Hola Unicoos
Me podeis ayudar a aplicar la definicion de derivada en esta funcion por favor?
Me cuesta porque no sé qué tengo que hacer con la h del denominador me he quedado atascada, quiero aplicar primero la fórmula general trabajando en sustituir (x+h) en las x de la funcion y luego sustituir el punto f(2) en la fórmula de sustituir el punto.
Me lo podrían explicar paso a paso? las dos fórmulas por separado?
Muchisimas gracias.
lbp_14
el 8/6/17
Neofito 007
el 8/6/17
lbp_14
el 8/6/17 -
Claudia
el 7/6/17Ayuda para calcular esta serie de Fourier
Facu Imfeld
el 8/6/17La he resuelto teniendo en cuenta la notación trigonométrica de Fourier y me quedó:
Ao = 1/3
An = [2cos(npi)]/(npi)^2
Bn = 1/npi
Intenta resolverla a ver que te queda, o envía tu procedimiento aquí y lo veo
Recuerda para simplificar expresiones en este tema:
Cos(npi) = (-1)^n aplica también si tienes cos(-npi)
Sen(npi) = 0 aplica también si tienes sen(-npi)
Te enviaría mi procedimiento pero mi internet es muy lento para la carga de imágenes
-
Orianna Marquez
el 7/6/17Buenas, tengo una duda como resuelvo la integral de senh^2 (x) cosh^2 (x) ??
La respuesta es -x/8 + 1/32 sech (4x) + c
NO SE COMO LLEGARON A LA SECANTE HIPERBOLICA POR FAVOR AYUDAA
-
Lili
el 7/6/17Unicoos, una preguntita de matrices,
ahí en el apartado A, para discutir el sistema habrán discutido también la matriz ampliada, no? Si la matriz ampliada tiene una línea entera de ceros, no es posible que tenga rango 3, entonces, como es posible que pongan que para cuando λ es desigual a 0 y a 2 el sistema es compatible determinado?
gracias
-
lbp_14
el 7/6/17Hola Unicoos,
Me pueden decir si tengo algun error en el estudio completo de esta funcion y ayudarme en el ultimo paso para calcular los puntos de inflexión, esque hay que hacer la tercera derivada para comprobar los posibles puntos de inflexion (aunque no haga falta mi profesora lo pide) y dice que hay que hacerlo como pone en la foto que os adjunto (es el papel que he puesto donde pone los pasos para calcular los ptos de inflexion y no sé hacer eso. Me podrian ayudar. Muchisimas gracias.
David
el 19/6/17Si f(x)=3x^4 +4x³-36x², la primera derivada es f'(x)=12x³+12x²-72x... Y la segunda derivada es f''(x)=36x²+24x-72.
Al igualarla a 0, te da dos posibles valores para los puntos de inflexión... x=(-1-√19)/3 y x=(-1+√19)/3
La tercera derivada es f''(x)=72x+24... SUSTITUYE LOS VALORES DE X OBTENIDOS EN ESA TERCERA DERIVADA...
Si te da distinto de cero (cosa que ocurre), los valores obtenidos son puntos de inflexion...
Te sugiero revises.. Crecimiento y curvatura de una función polinomica -
Julia
el 7/6/17
