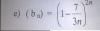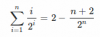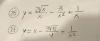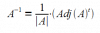-
Usuario eliminado
el 21/5/17Hola, ¿Cómo se plantearía un sistema de ecuaciones lineales con este contexto? Gracias.
Se desea recargar el cajero de un banco con billetes de 10, 20 y 50 euros. Por cada 5 billetes de 50 se ha de introducir 1 de 20, mientras que por cada 2 billetes de 20 se han de introducir 3 de 10.
Rubén
el 21/5/17Hola, Dana
Parece un enunciado incompleto, pero te digo cómo se haría. Definimos las variables:
x : número de billetes de 10 euros
y : número de billetes de 20 euros
z : número de billetes de 50 euros
Cuando dicen "Por cada 5 billetes de 50 se ha de introducir 1 de 20", teniendo en cuenta nuestras variables, se traduce en: z = 5y.
De igual manera, cuando dicen "Por cada 2 billetes de 20 se han de introducir 3 de 10", se traduce en 3y = 2x.
En cuanto al dinero que se tendría, que es lo que me parece que falta, sería 10x + 20y + 50z.
Espero haber ayudado!
Usuario eliminado
el 21/5/17Hola Rubén
El apartado a) de la pregunta, sólo con ese enunciado pide que plantees el problema como un SEL. El apartado b) pide que lo resuelvas con Cramer para encontrar la proporción de billetes. Se resolvería como un sistema compatible indeterminado? No es hasta el apartado c) que te dicen que el dinero es 28500 euros, dónde te piden el numero de billetes de cada uno.
Gracias!
Rubén
el 21/5/17Hola de nuevo!
En principio, el a) sí que sería plantear ese sistema de ecuaciones:
z - 5y = 0;
3y - 2x = 0;
Para el apartado b), sí se tendría que resolver como un SCI (Por rangos se ve que el sistema, efectivamente, es SCI). Cramer en principio es para sistemas SCD, pero podemos poner una variable como parámetro y resolver el sistema equivalente. Pongamos y = λ como parámetro, el sistema queda:
z = 5λ;
2x = 3λ;
Aunque las soluciones aquí son triviales habiendo escogido y como parámetro, resolvámoslo por Cramer:
det (A) = 0*0 - 1*2 = -2;
x = -3λ / (-2) = (3/2) λ
z = -10λ / (-2) = -5λ
En el apartado c) como te planteé, ahora sí, tenemos la siguiente ecuación:
10x + 20y + 50z = 28500
Con la solución encontrada en el apartado anterior, sustituimos:
15λ + 20λ + 250λ = 28500 -> λ = 100
Así, tenemos:
x = 150
y = 100
z = 500
Espero haber ayudado!
-
Mario Medina
el 21/5/17hola quisiera saber como se resuelve este ejercicio que por mi cuenta no puedo porque cuando hago el limite me queda 1 elevado a infinito
necesito que :
1)escribir los cuatro primeros terminos
2) indicar cotas y extremos
3) analizar su convergencia
-
Ixaulak Bane
el 21/5/17Hola, tengo varias dudas con las funciones, me he encontrado un problema y a raíz de él han surgido estas dudas:
Primero el problema:
ƒ(x)=x/x+1 y me preguntan si esta acotada. He estado viendo varios vídeos en Unicoos y creo que no me estoy quedando con lo esencial. Mis dudas son, ¿Como tengo que interpretar a x/x+1? ¿como una inecuación? ¿como una ecuación cualquiera? ¿como opero? ¿puedo simplificar x al estar en denominador y numerador? Seguramente es un ejercicio muy sencillo, pero es la primera vez que veo funciones y lo estoy haciendo por mi cuenta.
¿Alguien podría ayudarme y guiarme en cuanto a base y formas de proceder ante estos ejercicios?
Saludos
Rubén
el 21/5/17Hola, Ixualak
Sería importante de cara a resolver el ejercicio el uso de paréntesis, ya que tal como está escrito f(x) = 2. Supongo que es f(x) = x / (x+1), pero me gustaría que lo confirmaras ( ¡Si ese es el caso, no se puede simplificar x! ).
En general, si te preguntan si está acotada siempre es buena idea empezar haciendo los límites en ±infinito y por ambos lados dónde la función presente una discontinuidad.
Espero haber ayudado!
Rubén
el 21/5/17Ok, perfecto.
Respecto a si está acotada, depende de si te restringen el dominio para el ejercicio en particular. En principio, como no dicen lo contrario, supongo que te preguntan si está acotada sobre todo el dominio de la función. En este caso, al ser una fracción de funciones contínuas, los puntos que no son del dominio son dónde se anule el denominador. En este caso x = -1. Así, el dominio es: R \ {-1}.Si haces el límite cuando x tiende a -1 por la izquierda, ves que es infinito, por lo tanto no está acotada superiormente. De igual manera, al hacer el límite por la derecha, da -infinito, por lo que no está acotada inferiormente tampoco.Para este ejercicio ya estaría. Sin embargo, si no llegaras a ninguna conclusión analizando los puntos de discontinuidad, el siguiente paso sería hacer el límite cuando x tiende a ±infinito.Estos límites son los primeros que se deben mirar, en mi opinión, ya que si te dan un valor infinito ya sabes seguro que no estará acotada ( y probablemente te ayuden en otros posibles apartados dónde se estudien otras características de la función).Sin embargo, se puede hacer de otra manera y es suponiendo que sí está acotada por un valor k y tratar de buscar una x tal que x/ (x+1) > k. Si para toda k encuentras un valor posible de x, significa que no estará acotada.Y aún habría otra manera más, ya que la imagen de una función ( su recorrido ) es el dominio de la función inversa. Así, calculando la inversa y posteriormente su dominio sabes si está acotada o no. En este caso, la función inversa es x/ (1-x) y su dominio es R \ {1}, así se ve que puede tomar valores infinitamente grandes e infinitamente pequeños como hemos calculado antes.Disculpa haber escrito tanto, espero haberme explicado. Y espero haber ayudado! -
Guillem de la Calle
el 21/5/17Inducción
Para todo n≥1,
.Rubén
el 21/5/17Hola, Guillem
Como siempre al hacer inducción, comprobamos el caso base:
n = 1 -> 1/2 = 2 - 3/2 = 1/2
Ahora suponemos cierta la igualdad hasta n, y comprobamos si se verifica para n+1 operando sobre uno de los lados.
∑i=1n ( i / 2i ) + (n+1)/2n+1 => (Hipótesis de inducción) => 2 - (n+2)/2n + (n+1)/(2n+1) = 2 - ((n+2)*2 )/2n+1 + (n+1)/2n+1 = 2 + (-n-3)/2n+1 = 2 - (n+3)/2n+1
Y esto último, efectivamente, es lo que se obtiene al poner a la derecha de la igualdad n+1 en vez de n. Así, queda comprobado.
Espero haber ayudado!
-
Julien
el 21/5/17Hola ! No entiendo como derivar estas 2 funciones. En particular la parte con raizes. Muchas gracias !
-
Noé Muñoz Alonso
el 21/5/17En un ejercicio me dicen que demuestre que si para f:ℛ→ℛ, lím f(x) = L∈ℛ cuando x→0+, entonces lím f(1/x) = L∈ℛ cuando x→+∞. He hecho el ejercicio y me sale que el K real que debo tomar para que se verifique la tesis es (1/δ) pero no estoy seguro. ¿Es esto correcto?
Antonio Silvio Palmitano
el 21/5/17Tienes como hipótesis: Lím(x→0+) f(x) = L.
Luego, debes resolver:
Lím(x→+∞) f(1/x) =
(plantea la sustitución, o cambio de variable:
w = 1/x, de donde tienes: x = 1/w, y observa que cuando x tiende a +infinito tienes que w tiende a cero por la derecha),
luego sustituyes y queda:
= Lím(w→0+) f(w) = aplicamos la hipótesis = L.
Espero haberte ayudado.
-
Luis Viñedo
el 21/5/17No entiendo por qué cuando yo sustituyo esos mismos valores en la función me sale algo diferente en el apartado B de esta tabla. Se tiene que hacer de forma diferente a como se hace el el A?
Antonio Silvio Palmitano
el 21/5/17Observa que para hacer las evaluaciones para la función cuya expresión es g(x) = senx / x, debes utilizar la calculadora pero en radianes.
Por favor, verifica tus cálculos, porque es muy probable que éste haya sido tu inconveniente.
Luego, tienes que el límite para x tendiendo a cero de la función es igual a uno.
Espero haberte ayudado.
-
Juan Tomas
el 21/5/17Para que una matriz sea regular que tiene que ocurrir? Si me piden que la compruebe?
Victor
el 21/5/17Una matriz regular es una matriz cuadrada que tiene inversa.
Para realizar la matriz inversa ten presente esta fórmula:
Cuando el determinante de la matriz es igual a 0, la matriz no tiene inversa. Por lo tanto, para comprobar si tiene inversa debes hallar el determinante. Si no es = 0 entonces podrás encontrar la matriz pedida.
Tu ejercicio sí tiene inversa, su determinante es -1
-
lbp_14
el 21/5/17Hola Unicoos,
Algún vídeo o página que explique el concepto del por qué el estudio de los límites laterales? No cómo se resuelve, sino el concepto de por qué se hace.
Muchas gracias.
César
el 21/5/17En ocasiones las funciones en un punto no están definidas, siendo que por la izquierda tienen un valor y otro diferente por la derecha.
Es por eso la necesidad de calcular sus limites laterales .
Imagina la funcion f(x)=1/x en el punto x=0 a su izquierda el limite seria 1/0- =-∞ y por su derecha lim 1/0+ =+∞
ten en cuenta que 0- es un 0 ligeramente negativo -0.0000000000001 y 0+= 0.000000001
-
lbp_14
el 21/5/17Hola Unicoos,
Si tengo una fracción (4x6 /3) - (2x) , ya sé que habría que sacar factor común pero podría operar así?: 4x6 • 3-1 - 2x ?? Como podría multiplicarlo?
Muchísimas gracias
