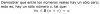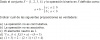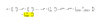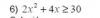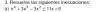-
Maths, cuando puedas me corriges esto, es para ir haciendo la tarea perfecta para que me puntúe el máximo para la nota. Te subo los dos primeros.

Ángel
el 28/4/17Antonio Silvio Palmitano
el 28/4/17Está todo correcto, Julio.
Solo vamos con una observación para el segundo ejercicio:
recuerda que la suma y la restas son operaciones entre vectores pero no entre puntos,
por lo que la forma de escribir los vectores es con restas componente a componente (llamamos u al primer vector y llamamos v al segundo vector):
u = AB = < 3 - 2 , 5 - (- 3) > = < 1 , 8 >,
v = CD =< - 1 - (- 2) , 0 - (- 4) > = < 1 , 4 >.
Espero haberte ayudado.
-
Saludos nuevamente chicos y a c/unicoo...
Alguien puede ayudar en un problemita, no se como resolver, ecuaciones, fracciones, relgla de tres.... etc
Gracias de antemano
Antonio Silvio Palmitano
el 28/4/17Comienza por expresar las dimensiones del piso del aula con números enteros, por lo que las expresamos en centímetros:
x = 4,2 m = 420 cm (ancho),
y = 14 m = 1400 cm (largo),
y la superficie del piso:
S = x*y = 420*1400 = 588000 cm2.
Luego, descomponemos a x e y en factores primos:
x = 420 = 22*3*5*7,
y = 1400 = 23*52*7.
Luego planteamos el Máximo Común Divisor entre 420 y 1400 (recuerda que es el producto de todos los factores comunes a ambos números, tomados con sus menores exponentes):
a = MCD(420,1400) = 22*5*7 = 140 cm,
que es la longitud de la arista de la mayor baldosa que podemos utilizar para cubrir el piso del aula sin cortar baldosas,
y observa que la superficie que cubre una baldosa es:
Z = a2 = 1402= .19600 cm2.
Luego, para determinar la cantidad de baldosas a utilizar queda:
N = S/Z = 588000/19600 = 30 baldosas,
cuyas cantidades, distribuidas a lo ancho y a lo largo del piso del aula son:
Nx = x/a = 420/1140 = 3 baldosas (a lo ancho),
Ny = x/a = 1400/140 = 10 baldosas ( a lo largo).
Espero haberte ayudado.
-
Hola... Me pueden ayudar...
La respuesta me parece que es la a.)
¿Esta bien?
Gracias a quien me responda.
Antonio Silvio Palmitano
el 28/4/17Observa que tienes un rectángulo dividido en 18 cuadrados, de los cuáles 10 están sombreados y 8 están blancos,
luego, la razón entre la cantidad de cuadrados sombreados y la cantidad total de cuadrados es:
r = 10/18 = 5/9.
Luego, observa que los círculos tienen una parte sombreada, que comprende un ángulo con vértice en su centro cuya medida designamos x,
y recuerda que cada círculo completo comprende un ángulo con vértice en su centro cuya medida es 360°,
luego planteamos la razón entre los ángulos que hemos nombrado para un círculo:
x/360° = r, reemplazamos el valor remarcado y queda:
x/360° = 5/9, hacemos pasaje de divisor como factor y queda:
x = (5/9)*360° = 200°.
Observa que a medio círculo le corresponde 180°, por lo que tienes un poco más que medio círculo,
por lo que concluimos que la opción D es la respuesta correcta.
Espero haberte ayudado.
-
Buen Día
Alguien me puede ayudar demostrando lo que me piden, creo que para demostrar se deben usar cuantificadores y conjuntos, entre otros símbolos matemáticos usados en lógica.
-muchas gracias
Antonio Silvio Palmitano
el 28/4/17Vamos con una orientación.
Puedes comenzar por suponer que existen dos ceros distintos: c ≠ c1 (supuesto absurdo).
Luego tienes:
a + c = a, por ser c un cero para la suma,
a + c1 = a, por ser c1 un cero para la suma,
luego restas miembro a miembro en ambas ecuaciones y tienes:
(a + c) - (a + c1) = a - a, distribuyes agrupamientos y queda:
a + c - a - c1 = a - a, cancelas términos opuestos en ambos miembros y queda (recuerda que c es un cero para la suma):
c - c1 = c, sumas c1 en ambos miembros y queda:
c - c1 + c1 = c + c1, cancelas términos opuestos en el primer miembro y queda:
c = c + c1, luego en el segundo miembro tienes (recuerda que c es un cero para la suma):
c = c1.
Luego, como has llegado a contradecir el supuesto absurdo inicial tienes que el supuesto inicial es Falso y que, por lo tanto, c es igual a c1,
y el cero de la suma con números reales es único.
Espero haberte ayudado.
Espero haberte ayudado.
-
Hola... Necesite que alguien me pueda ayudar en el problema de que trata de una operación binaria... (NO COMPRENDO MUY BIEN ESTE TEMA)
OS RUEGO AYUDA
Gracias de antemano...
David
el 30/4/17Me encantaría ayudarte, pero no respondo dudas universitarias que no tengan que ver específicamente con los videos que ya he grabado como excepcion. O de otras asignaturas que no sean matemáticas, física y química. Lo siento de corazón… Espero lo entiendas
Ojalá algun unicoo universitario se anime a ayudarte (de hecho lo ideal es que todos los universitarios intentarais ayudaros los unos a los otros)
-
Antonio Silvio Palmitano
el 28/4/17Tienes que el Perímetro del cuadrado es 12, por lo que la longitud de su lado es a = 3.
Tienes los vértices: A(1,0,1) y B(2,2,3).
Puedes plantear para que el tercer vértice es C(x,y,z).
Y para el cuarto vértice tienes que sus coordenadas son: D(0,w,0), ya que pertenece al plano coordenado OXZ.
Luego, como los vértices son consecutivos, puedes plantear:
|AB| = 3, que puedes verificar que se cumple,
|BC| = 3,
|CD| = 3,
|DA| = 3.
Desarrollamos en la cuarta ecuación y queda:
√( (0-1)2+(w-0)2+(0-1)2 ) = 3, resolvemos el argumento de la raíz y queda:
√(w2 + 2) = 3, hacemos pasaje de raíz como potencia y queda:
w2 + 2 = 9, hacemos pasaje de término y queda:
w2 = 7, de donde tenemos dos opciones:
1) w = - √(7), que nos conduce al punto de coordenadas: D1(0,- √(7),0);
2) w = √(7), que nos conduce al punto de coordenadas: D2(0,√(7),0).
Luego, haz un dibujo del cuadrado, y verás que los vectores:
u = AD y v = BC son paralelos con igual sentido, por lo que puedes plantear que sus componentes son iguales:
v = u, expresamos los vectores para cada opción:
1)
BC1 = AD1, expresamos a los vectores con sus componentes:
<x-2,y-2,z-3> = <0-1,-√(7)-0,0-1>, resolvemos componentes en el segundo miembro y queda:
<x-2,y-2,z-3> = <-1,-√(7),-1>, igualamos componente a componente y queda el sistema de ecuaciones:
x - 2 = - 1, de donde despejamos: x = 1,
y - 2 = - √(7), de donde despejamos: y = 2 - √(7),
z - 3 = - 1, de donde despejamos: z = 2,
por lo que tenemos que las coordenadas del tercer vértice son: C1(1,2-√(7),2);
2)
BC2 = AD2, expresamos a los vectores con sus componentes:
<x-2,y-2,z-3> = <0-1,√(7)-0,0-1>, resolvemos componentes en el segundo miembro y queda:
<x-2,y-2,z-3> = <-1,√(7),-1>, igualamos componente a componente y queda el sistema de ecuaciones:
x - 2 = - 1, de donde despejamos: x = 1,
y - 2 = √(7), de donde despejamos: y = 2 + √(7),
z - 3 = - 1, de donde despejamos: z = 2,
por lo que tenemos que las coordenadas del tercer vértice son: C2(1,2+√(7),2).
Espero haberte ayudado.
-
Hola!!
Buen día amigos de unicoos...
Podrían alguien por favor ayudarme en el problema que está en la imagen...
Se los agrdezco. Gracias
Alvaro
el 28/4/17 -
Alguien me puede ayudar con estos dos ejercicios por favor? Que quede como intervalo como {xER/......} GRACIAS
Ángel
el 28/4/172x2+4x≥30
2x2+4x-30≥0
Haciendo 2x2+4x-30=0 obtenemos x1=3 y x2=-5, por lo que:
(x-3)(x+5)≥0
Tenemos que ver entre los intervalos (-inf,-5) (-5,3) (3,inf) en los que el signo sea positivo para la desigualdad (es decir, en los que el signo de un factor y otro coincida)
*En el intervalo (-inf,-5) el factor (x-3) será negativo y el (x-5) también, al multiplicar - por - obtenemos un más (incluido en nuestra solución por cumplir la desigualdad)
*En el intervalo (-5,3) el factor (x-3) será negativo y el otro positivo, al multiplicar + por - obtenemos un menos (no es incluido en nuestra solución por no cumplir la desigualdad)
*En el intervalo (3,inf) el factor (x-3) será positivo y el otro también, al multiplicar + por + obtenemos un más (incluido en nuestra solución por cumplir la desigualdad)
Estos intervalos cumplen que 2x2+4x-30>0 y x1 y x2 cumplen 2x2+4x-30=0, por lo que 2x2+4x-30≥0 es la unión de ambas condiciones (por eso los corchetes[ ] para incluir dichas raíces):
x∈(-inf,-5] ∪ [3,inf) = x∈ℛ - {(-5,3)}
Ángel
el 28/4/17x4+3x3-3x2≤11x+6
x4+3x3-3x2-11x-6≤0
Haciendo RUFFINI obtenemos x1=-1, x2=-1, x3=-3, x4=2 por lo que:
(x+1)(x+1)(x+3)(x-2)≤0
Tenemos que ver entre los intervalos (-inf,-3) (-3,-1) (2,3) (3,inf)en los que el signo sea negativo para la desigualdad (es decir, que de los cuatro intervalos sean impares los factores negativos)
*En el intervalo (-inf,-3) los 4 factores serían negativos, por lo que obtenemos un más (no incluido por no cumplir la desigualdad)
*En el intervalo (-3,-1) el factor (x-3) será negativo y los otros positivos (nº impar de factores negativos), por lo que obtenemos un menos (incluido en nuestra solución por cumplir la desigualdad)
*En el intervalo (-1,2) los factores (x+1) sólo tenemos UN negativo en (x-2) , por lo que obtenemos un menos (incluido en nuestra solución por cumplir la desigualdad)
*En el intervalo (2,inf) los 4 factores serán positivos, por lo que obtenemos un más (no incluido por no cumplir la desigualdad)
Los intervalos resaltados cumplen que x4+3x3-3x2-11x-6<0 y x1=-1, x2=-1, x3=-3, x4=2 cumplen x4+3x3-3x2-11x-6=0, por lo que x4+3x3-3x2-11x-6≤0 es la unión de ambas condiciones (por eso los corchetes[ ] para incluir dichas raíces):
x∈ {-3} ∪ (-3,-1) ∪ {-1} ∪ (-1,2) ∪ {2} = x∈[-3,2] = x∈ℛ - {(-inf,-3)U(2,inf)}