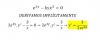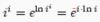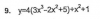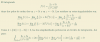-
Buenas tardes (x+a)1/2 ademas de ser la raiz cuadrada de x+a ¿se podria desarrollar el binomio como x1/2 + a 1/2 +1/2xa?
Antonio
el 27/4/17 -
Alvaro
el 27/4/17Verás, para este ejercicio es importante tener presente que la derivada no es mas que la ecuación de la pendiente de la recta tangente a una curva en un punto, primero, como sabemos que esa recta y=x+1 es tangente a la función f(x), en x=1, y tanto la recta como la función f(x), al ser evaluadas en x=1 deben tomar los mismos valores, pero OJO solo en ese punto donde es tangente, de donde vas a obtener una ecuación con a y b como incógnitas, ahora si nosotros derivamos la función f(x) con respecto a x, y la evaluamos en el mismo punto x=1 lo que estaremos hallando es la pendiente de la recta tangente a f(x) en dicho punto, pero como y es su recta tangente en x=1 y tiene la forma y=mx+b, donde la pendiente m=1, entonces podremos obtener la segunda ecuación, con lo que tendríamos un sistemas de ecuaciones con dos incógnitas, a y b.
-
Alvaro
el 27/4/17Ahí te estoy enviando, el primero está resuelto completamente, el segundo te envio la forma de plantearlo, lo que debes hacer es plantear tus matrices A y B con las mismas dimensiones de M y N puesto que deben tener las mismas dimensiones para sumarlas, y luego solo una vez que has partido de las condiciones dadas, generas varios sistemas de ecuaciones con dos incógnitas de modo que puedas encontrar cada par de términos en cada matriz A y B, ahi te muestro las forma de plantear las ecuaciones. Saludos.
-
Muy buenas tardes, os pongo un ejercicio por si puede alguien echarme una mano... Gracias de antemano.
El resultado, según el solucionario es de (10πi)/27 pero a mi me sale 0. ¿Estoy en lo cierto?
Muchas gracias. Un saludo